Геометричне рішення ОЗЛП.

Якщоn - m = 2, то задача може бути геометрично вирішена в осях координат.

При n - m ³ 3 - задача вирішується аналітично.

Оскільки х₁ ³ 0 і х₂ ³ 0,тоодразу можна обмежити ділянку площини (рис.1).

х₃ ³ 0. Розглянемо граничний випадок, коли х₃ = 0, тобто 80 – х₁ – х₂ = 0. Графічним зображенням цього рівняння є пряма лінія, котра поділяє всю площину на дві півплощини, в одній з яких
х₃ > 0, а в другій х₃ < 0.

Розрахуємо координати та побудуємо пряму (рис.1):

80 – х₁ – х₂ = 0 Þ х₁ + х₂ = 80

х₁ = 0 х₂ = 80 х₁ = 80 х₂ = 0

Після цього визначається півплощина в якій х₃ > 0.

Розглянемо граничний випадок, коли у₁ = 0, тобто –1 + 0.1 х₁ – 0.1х₂ = 0 ´10

–10 + х₁ – х₂ = 0 Þ х₁ – х₂ =10

х₁ = 10 х₂ = 0 х₁ = 60 х₂ = 50

Розглянемо граничний випадок, коли у₂ = 0, тобто 35 – х₁ = 0 або х₁ =35

Розглянемо граничний випадок, коли у₃ = 0, тобто 40 – х₂ = 0 або х₂ =40

Розглянемо граничний випадок, коли у₄ = 0, тобто –30 + х₁ + х₂ = 0

х₁ + х₂ =30

х₁ = 0 х₂ = 30 х₁ = 30 х₂ = 0

Рис. 1.

В результаті отримуємо ОБЛАСТЬ ДОПУСТИМИХ РІШЕНЬ(ОДР), усередині якої лежить множина допустимих рішень, а за її межами хоч одна змінна – від’ємна.

Після цього знаходимо оптимальне рішення.

Очевидно, що функція 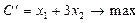при тих самих х₁ та х₂, що і С.

При С’ х₁ + 3х₂=0 Þ х₁ = 0 х₂ = 0 х₂ = 10 х₁ = –30

На цій прямій ставимо стрілки, які вказують напрямок, в якому збільшуються значення функції. Максимум отримуємо у верхній точці ОДР (тобто отримуємо оптимальне рішення).

Дана вершина утворюється на перехрещенні прямих

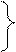
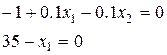
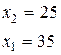Þ

Таким чином, рішення задачі:

х₁ = 35 х₂ = 25 х₃=80-25-35=20

Максимальний доход від розвантаження вагонів отримуємо при такому розподіленні за фронтами: на 1-й ВФ – 35 вагонів, на 2-й ВФ – 25 вагонів, на 3-й ВФ – 20 вагонів. При цьому доход – С=160+35+3*25=270грн.