ЛекцІя №5 транспортна задача ЛІНІЙНОГО ПРОГРАМУВАННЯ

1. Постановка задачі.

Симплекс-метод вирішення ОЗЛП являється універсальним і може бути застосованим для рішення будь-яких задач такого типу. Однак існують деякі типи задач лінійного програмування, які допускають більш просте рішення. До таких задач відноситься транспортна задача.

Нехай є m пунктів відправлення (ПВ) A₁, A₂, … A_m, в яких сконцентровані запаси певного однорідного вантажу в кількості, відповідно a₁, a₂, … a_m одиниць. Також є n пунктів призначення (ПП) B₁, B₂, … B_n з потребами у цьому вантажі, відповідно: b₁, b₂, … b_n одиниць.

Припускається, що 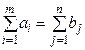(транспортна задача є „закрита” або „збалансована”). Відома вартість c_ij перевезення одиниці вантажу від кожного пункту відправлення A_i до кожного пункту призначення B_j. Таблиця (матриця) вартості c_ij перевезень задана:

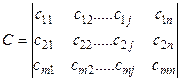
Необхідно скласти такий план перевезень, при якому всі потреби у вантажі були б виконані, а загальна вартість перевезень була б мінімальна. Така постановка являє собою транспортну задачу по критерію вартості (можлива по критерію часу).

2. Формалізація задачі.

Введемо позначення:

x_ij – кількість вантажу, що відправляється з i-го пункту відправлення A_i в j-й пункт призначення B_j. Невід’ємні значення x_ij (кількість яких m×n) повинні задовольняти наступним умовам (обмеженням):

1) загальна кількість вантажу, що направляється з кожного пункту відправлення в усі пункти призначення, повинна дорівнювати запасу вантажу в цьому ПВ, тобто:

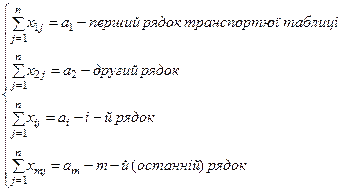(1)

2) загальна кількість вантажу, що доставляється в кожний ПП з усіх ПВ, повинна дорівнювати потребам цього ПП., тобто:

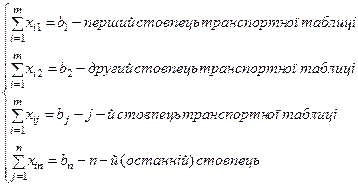(2)

3) Загальна вартість всіх перевезень повинна бути мінімальною, тобто:

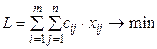
Функція L та обмеження (1) і (2) лінійні, так що це є типова задача лінійного програмування. Особливості транспортної задачі дозволяють вирішити її більш простим способом, ніж симплекс-методом:

1) всі коефіцієнти при змінних в обмеженнях (1) і (2) дорівнюють 1;

2) не всі з m+n є незалежними, оскільки 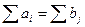, через що в транспортній задачі базисних змінних m+n–1, а вільних mn – (m+n-1) = (m-1)(n-1).

3. Основні визначення.

1) значення x_ij одиниць вантажу, що направляється з пункту відправлення A_i в пункт призначення B_j будемо називати перевезенням.

2) будь-яку сукупність значень x_ij будемо називати планом перевезень.

3) план перевезень будемо називати допустимим, якщо він задовольняє балансовим умовам (1) і (2) – всі запаси вивезені, всі потреби задовільнено.

4) допустимий план перевезень будемо називати опорним, якщо в ньому ненульових перевезень (базисних змінних x_ij) r = m+n–1, а інші перевезення (змінні) дорівнюють нулю.

5) план перевезень будемо називати оптимальним, якщо він серед всіх допустимих планів призводить до найменшої загальної вартості перевезень.

4. Транспортна таблиця.

На відміну від симплекс-метода, вирішення транспортної задачі зводиться до більш простих операцій, які виконуються в таблиці, що називається транспортною(табл. 1). В такій таблиці в певному порядку записують умови транспортної задачі, в т.ч.:

1) пункти відправлення A_i та пункти призначення B_j. При цьому кожному з m рядків ставиться у відповідність певний ПВ A_i, а кожному стовпцю – певний ПП B_j;

2) запаси вантажу a_i, що є в кожному пункті відправлення записуються в останньому стовпці;

3) потреби у вантажі b_j, що є в кожному пункті призначення записуються в останній рядок;

4) вартість перевезення c_ij одиниці вантажу з кожного ПВ A_i в кожний ПП B_j записуються в верхньому лівому кутку клітини на перетині відповідних i-го рядка та j-го стовпця.

5) кількість одиниць вантажу x_ij, що перевозиться з ПВ A_i в ПП B_j записується у відповідній клітині у правому нижньому куті.

Таблиця 1

	B1	B2	...	Bj	...	Bn	Запаси ai
A1	c11 x11	c12 x12		c1j x1j		c1n x1n	a1
A2	c21 x21	c22 x22		c2j x2j		c2n x2n	a2
…							…
Ai	ci1 xi1	ci2 xi2		cij xij		cin xin	ai
…							…
Am	cm1 xm1	cm2 xm2		cmj xmj		cmn xmn	am
Потреби bj	b1	b2	…	bj	…	bn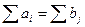

Клітини транспортної таблиці, в яких записані відмінні від нуля перевезення називаються базисними, інші (порожні) – вільні. Кількість базисних клітин в опорному, а, значить, і в оптимальному, плані має бути r = m+n–1.

Таким чином, рішення транспортної задачі зводиться до наступного: знайти такі невід’ємні значення перевезень (базисних змінних), які б задовольняли таким умовам:

1) сума перевезень по кожному рядку повинна дорівнювати запасу вантажу у даному пункті відправлення;

2) сума перевезень по кожному стовпцю повинна дорівнювати потребам відповідного пункту призначення;

3) загальна вартість усіх перевезень повинна бути мінімальною.

Транспортна таблиця з порушенням балансу.

Якщо сумарні запаси вантажу у пунктах відправлення не співпадають з сумарними потребами в цьому вантажі в пунктах призначення, то має місце відкрита транспортна задача. Відкриту транспортну задачу зводять до закритої шляхом введення фіктивного пункту призначення або пункту відправлення.

1) транспортна задача з надлишком запасів: 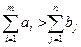. В цьому випадку вводять фіктивний пункт призначення B_ф (додатковий стовпець) з потребами: 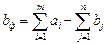, вартість перевезення одиниці вантажу в фіктивний пункт призначення c_iф=0. Перевезення x_iф з A_i в B_ф означає, що в пункті відправлення A_i залишились невикористані (невідправлені) запаси вантажу у кількості x_iф одиниць.

2) транспортна задача з надлишком потреб: 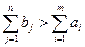. В цьому випадку вводять фіктивний пункт відправлення A_ф (додатковий рядок) з запасами: 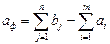, вартість перевезення одиниці вантажу з фіктивного пункту відправлення c_фj=0. Перевезення x_фj з A_ф в B_j означає, що в пункті призначення B_j частина потреб у розмірі x_фj одиниць вантажу залишилась непокрита.

5. Знаходження опорного плану перевезень у транспортній таблиці.

Існує декілька методів знаходження опорного (початкового) плану перевезень:

1) північно-східного кута – застосовується частіше при виконанні розрахунків на ЕОМ;

2) метод найменшої вартості;

3) метод подвійної переваги – дозволяє отримати план перевезень досить близький до оптимального і скоротити обсяг розрахунків у порівнянні з методом північно-східного кута у середньому на 20-25%.

Суть вказаних методів у тому, щоб розподілити всі запаси вантажу і задовольнити всі потреби в ньому, при цьому кількість базисних (зайнятих) клітин має бути не більш, ніж r = m+n–1.