Метод подвійної переваги
У кожному з рядків транспортної таблиці необхідно знайти клітину з мінімальною вартістю позначити його знаком *. Потім те ж потрібно виконати в кожному стовпці. Деякі клітини (відзначені **) мають мінімальні значення як по рядку, так і по стовпці. В такі клітини записується максимально можливі перевезення, виключаючи із розгляду після кожного запису xij, відповідно, рядок або стовпець. Далі в частині матриці, що залишилася, записується максимально можливі перевезення в клоітини, відзначені знаком *. Після цього заповнюються непомічені клітини. Приклад одержання початкового плану приведено в табл. 2-8.
Таблиця 2-8
| ** | * | * | * |
| * | |||
| * |
Призначимо перевезення в клітини, позначені **.
| Ai | |||||
| 2 ** | 3 * | 4 * | 5 * | | |
| 6 * | |||||
| 9 * | |||||
| bj | |
Призначимо перевезення в клітини, позначені *.
| ai | |||||
| 2 ** | 3 * | 4 * | 5 * | | |
| 6 * | |||||
| 9 * | |||||
| bj | | |
| ai | |||||
| 2 ** | 3 * | 4 * | 5 * | | |
| 6 * | | ||||
| 9 * | |||||
| bj | | | |
Призначимо перевезення в клітини, що залишились.
| Ai | |||||
| 2 ** | 3 * | 4 * | 5 * | | |
| 6 * | | ||||
| 9 * | | ||||
| bj | | | |
| Ai | |||||
| 2 ** | 3 * | 4 * | 5 * | | |
| 6 * | | ||||
| 9 * | | ||||
| bj | | | | |
| Ai | |||||
| 2 ** | 3 * | 4 * | 5 * | | |
| 6 * | | ||||
| 9 * | | ||||
| bj | | | | |
| ai | |||||
| 2 ** | 3 * | 4 * | 5 * | ||
| 6 * | |||||
| 9 * | |||||
| bj |
У даному початковому плані 6 базисних кліток, що відповідає числу постачальників і споживачів: 4+3-1=6. Якщо число базисних кліток більше m+n-1, то допущені помилки при складанні початкового плану. Якщо число базисних кліток менше m+n-1, то має місце випадок виродження. Загальна вартість виконання перевезень L=2·20+3·10+6·20+11·20+13·15+15·5=680 грн.
Випадок виродження початкового плану.
При вирішенні практичних задач можуть мати місце випадки, коли число базисних клітин менше m+n-1. В цьому випадку має місце випадок виродження. Виродження може статись, якщо призначення чергового перевезення призводить до одночасного виключення рядка і стовпця транспортної таблиці. Для побудови оптимального плану методом потенціалів необхідно збільшити число базисних кліток до m+n-1, уводячи "штучні нульові перевезення". Приклад складання початкового плану у випадку "виродження" наведено в табл. 9-11.
Призначимо перевезення x11=20. В цьому випадку потреби пункту b1 будуть повністю покриті за рахунок a1 і з таблиці виключається перший рядок і перший стовпець. Помітимо цю клітину буквою В.
| Ai | ||||
| 2 ** В 20 | 4 * | 5 * | | |
| 6 * | ||||
| 9 * | ||||
| bj | |
Далі призначимо перевезення методом подвійної переваги. Останню заповнену клітину позначимо буквою П.
| Ai | ||||
| 2 ** В 20 | 4 * | 5 * | | |
| 6 * | | |||
| 9 * | П 5 | | ||
| bj | | | |
В цій таблиці 4 базисних клітини, а повинно бути 3+3-1=5. Для того, щоб довести число базисних клітин до 5 призначаємо штучне нульове перевезення в клітину, що знаходиться на перетині рядка з міткою В та стовпця з міткою П, або стовпця з міткою В та рядка з міткою П:
| Ai | ||||
| 2 ** В 20 | 4 * | 5 * | | |
| 6 * | | |||
| 9 * | П 5 | | ||
| bj | | | |
6. Знаходження оптимального плану перевезень у транспортній таблиці.
Побудований опорний план перевезень необхідно перевірити на оптимальність. Це можна виконати за допомогою методу потенціалів. Потенціали представляють собою умовну суму, яку вносить кожний з пунктів призначення Ai (потенціал Ui) та кожний з пунктів призначення Bj (потенціал Vj) за перевезення одиниці вантажу деякому перевізнику. Всього потенціалів m+n.
Значення одного з потенціалів приймається довільним (звичайно нуль). Значення інших потенціалів розраховується по базисним (заповненим) клітинам таким чином, щоб для всіх базисних клітин виконувалась умова:
Ui + Vj=cij (3)
План перевезень буде оптимальним, якщо для всіх базисних клітин виконується умова (3), а для всіх вільних умова:
Ui + Vj ≤ cij (4)
Якщо умова (4) не виконується, то отримане рішення (план перевезень) необхідно покращити. Для цього потрібно перерозподілити вантажопотоки (перевезення) таким чином, щоб клітина з найбільшим порушенням умови (4) була включена в план перевезень, тобто стала базисною. Однак, поява перевезення в вільній клітині повинно компенсуватись зміною значень в інших базисних клітинах. З цією метою будується цикл перерахування.
1) цикл перерахування будується для вільної клітини, де порушення умови (4) буде максимальним, тобто: Ui + Vj – cij = max.
Цикл будується таким чином, щоб всі його вершини, крім початкової (вільної клітини), знаходились в базисних (зайнятих) клітинах. При цьому в кожній вершині виконується поворот на 90º. Цикли перерахування можуть приймати наступні форми:

2) вільну клітина, що вводиться в план перевезень, помічається знаком „+”. Далі по черзі помічаються всі базисні клітини циклу знаками „–“ та „+” і т.д.
3) клітина, що помічена „–“, яка має найменше значення перевезення X*, повинна бути виключена з базису і стати вільною.
4) обсяги перевезень в клітинах, помічених знаком „+”, збільшується на величину X *, а в клітинах, помічених знаком „–”, зменшується на цю величину.
5) після перерозподілу перевезень і зміни базису будується нова транспортна таблиця (план перевезень), яка знову перевіряється на оптимальність методом потенціалів.
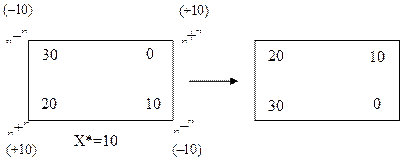
Нижче наведено приклад розрахунку потенціалів та пошуку оптимального плану перевезень.
Дата добавления: 2015-12-22; просмотров: 1331;
