Розглянемо цей метод на прикладі задачі ведення поїзда по дільниці.

Рух поїзда по дільниці завдяки дії різних факторів відбувається зі змінною швидкістю.

Операція розбивається на декілька кроків, на кожному з яких приймається рішення від якого залежить успіх даного кроку і всієї операції в цілому. Таке рішення називають управлінням на і-му кроці.

Управління операцією в цілому являє собою сукупність всіх покрокових управлінь.

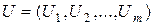
де U_і – управління на і-му кроці.

Ефект операції залежить від управління операцією:

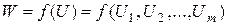
Виникає питання– як вибрати покрокові управління U₁, U₂, ..., U_m, щоб ефект був максимальним.

При цьому ефект від операції:

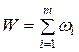
де w_і – ефект на і-му кроці.

Суть динамічного програмування в тому, що операція здійснюється поетапно (або покроково). Трудність полягає в тому, що результат управління на кожному кроці впливає на всі подальші кроки. Це слушно для всіх кроків, крім останнього.

Процес динамічного програмування здійснюється від кінця операції до її початку.

Трудність в тому, що при оптимізації останнього n-го кроку невідомо, як закінчився n-1 крок (невідомий стан системи перед останнім кроком).

Для того, щоб вийти з цього забруднення, робляться припущення по результатам n-1 кроку про стан системи. Таке припущення називають умовно-оптимальним.

Рухаючись від кінця до початку можна знайти умовно-оптимальне рішення, яке забезпече оптимальне продовження процесу відносно стану, який досягнуто в даний момент.

Після цього, якщо відомий початковий стан системи, можна знайти безумовно оптимальне рішення на першому кроці. Після першого кроку система перейде в другий стан, для якого нам вже також відомо оптимальне управління.

Таким чином, в процесі оптимізації управління методом динамічного програмування багатокроковий процес проходиться двічі. Перший раз – від початку до кінця, внаслідок чого визначаються умовно-оптимальні управління на кожному кроці, а також умовно-оптимальний ефект на етапі від даного кроку і до кінця операції.

Другий раз проходимо процес від начала до кінця, внаслідок чого визначаємо безумовні оптимальні крокові управління на всіх кроках операції.

Приклад

Умова

Треба провести поїзд по дільниці з мінімальними витратами палива або електроенергії.

Швидкості руху поїздів та таблиці витрат отримані на підставі тягових розрахунків.

Швидкість поїзду на початку та в кінці дільниці дорівнює 0. Швидкість поїзда в кінці кожного кроку може прийняти три різних значення.

Розв’язання

Перший етап.

1. Припустимо, що перед останнім кроком швидкість поїзда дорівнює V₃₁. Режим єдиний і він же оптимальний; витрати складають 70 одиниць.

4 (четвертий) крок : V₃₁®V₄ – оптимально 70 одиниць

Аналогічно і для V₃₂ та V₃₃

V₃₂®V₄ – оптимально 60 одиниць

V₃₃®V₄ – оптимально 50 одиниць

2. Переходемо до передостаннього кроку.

Припустимо, що на початку цього кроку швидкість дорівнює V₂₁. Можливі режими – V₂₁®V₃₁, V₂₁®V₃₂, V₂₁®V₃₃, при яких будуть різні витрати. Але на передостанньому кроці треба знайти таке управління, яке б забезпечувало максимальний ефект до кінця останнього кроку.

Знаходими витрати енергії на 3 + 4 кроках:

V₂₁®V₃₁®V₄ – 70+70=140 одиниць

V₂₁®V₃₂®V₄ – 50+60=110 одиниць

V₂₁®V₃₃®V₄ – 30+50= 80 одиниць (min)

умовно-оптимальний режим

Аналогічно розглядаємо можливі режими і для V₂₂ та V₂₃.

Таким чином проходимо зворотнім ходом до початку дільниці.

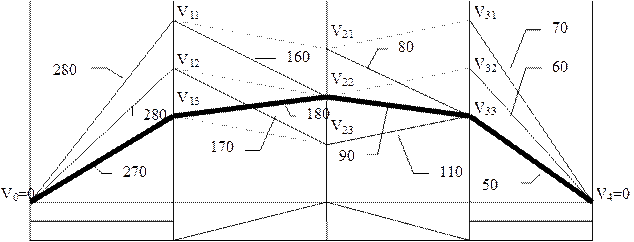
Зручно розв’язувати цю задачу у табличному вигляді. При цьому, в знаменнику таблиці наводяться витрати до кінця дільниці. З них обирається найменше значення і цей режим є умовно оптимальним.

Другий етап.

Починаємо рух від першого кроку до останнього для вибору дійсно оптимального рішення. Воно буде при мінімальних сумарних витратах, які записані на першому кроці.

V₁₁

V₁₂

V₁₃

V₂₁

V₂₂

V₂₃

V₃₁

V₃₂

V₃₃

V₄

V₁₁

V₂₁

V₃₁

V₀

V₁₂

V₂₂

V₃₂

V₁₃

V₂₃

V₃₃

	V₁₁	V₁₂	V₁₃		V₂₁	V₂₂	V₂₃		V₃₁	V₃₂	V₃₃		V₄
				V₁₁	90	70	60	V₂₁	70	50	30	V₃₁
V₀	120	110	90	V₁₂	110	90	60	V₂₂	80	60	40 90	V₃₂
				V₁₃	110	90	80	V₂₃	90	70	60	V₃₃	50

Таким чином, оптимальний варіант руху поїзда V₀® V₁₃®V₂₂®V₃₃®V₄, при якому витрати становлять 270 одиниць.

ЛЕКЦІЯ 8

СІТЬОВЕ ПЛАНУВАННЯ ТА УПРАВЛІННЯ

Загальні відомості

Сітьове планування та управління (СПУ) є одним з ефективних методів організації складних комплексів взаємопов’язаних робіт. В основі СПУ лежить сітьовий графік – модель виробничого процесу в вигляді мережі, тобто фігури, яка складається з вершин і ребер. Вершини – події, що визначають можливість початку чи закінчення різноманітних робіт, а ребра – технологічні операції (роботи), що складають виробничий процес. Події на графіку позначають кружками, а роботи – стрілками. Події нумерують послідовно. Кожну роботу позначають власним номером, чи номерами подій, що її обмежують. Цифри на стрілках означають номер роботи та її тривалість. Будь яка послідовність робіт складає шлях.

Перед побудовою сітьових графіків виконується аналіз технологічного процесу і встановлюється перелік робіт. Для кожної роботи визначають тривалість та попередні роботи, тобто ті роботи які повинні бути виконані до початку даної. На підставі цих даних складають структурно-часові таблиці.

<7 8 9 101112 13 >

Дата добавления: 2015-12-22; просмотров: 787;