Лекція 4. Симплекс-метод вирiшення задач лінiйного програмування. Табличний алгоритм пошуку оптимального рiшення ОЗЛП.

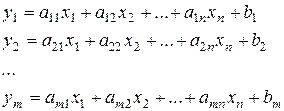
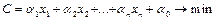
Одне з рішень (допустимих):

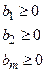
Якщо знайдено допустиме рішення, то для його покращення необхідно зменшити С. x_j зменшити не можна. Тому зменшити С можна тільки в тому випадку, якщо збільшити значення х_j з від’ємним коефіцієнтом a_j. Тобто якщо всі коефіцієнти С будуть додатні , то отримане рішення буде оптимальним.

Для покращення рішення вільну змінну x_j з від’ємним коефіцієнтом у цільовій вункції необхідно зробити базисною (>0), а ту в свою чергу – вільною (заміна змінних). Міняти вільну змінну треба на ту з базисних, котра раніше за інших обернеться в 0 при даному значенні x_j.Вибір залежить від мінімуму 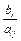{наприклад 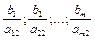для збільшення х₂}.

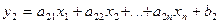Наприклад, міняємо х₂ нау₂ (якщо ). Для заміни необхідно вирішити рівняння відносно попередньої вільної змінної х₂. Отримаємо:

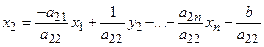
Потім необхідно підставити значення х₂ у всі інші рівняння системи і цільову функцію. Після приведення подібних отримаємо m рівнянь з у₂ замість х₂.

Для полегшення розрахунків ці перетворення щодо заміни змінних було виконано аналітично в загальному вигляді, а потім з них вивели правило, яке дозволяє автоматично робити заміну.Було отримано табличний алгоритм заміни змінних, в якому всі дії виконуються не з рівняннями, а з таблицями коефіцієнтів рівнянь.

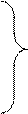Для того, щоб скласти цю таблицю необхідно всі рівняння та цільову функцію привести до вигляду:

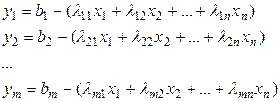l₁₁ = – a₁₁

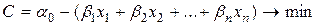b₁ = – a₁

Вільні змінні

Цільова функція	Вільні члени	х1	х2	...	хn
C	a0	b1	b2	...	bn
у1	b1	l11	l12	...	l1n
Базисні перемінні у2	b2	l21	l22	...	l2n
...	...	...	...	...	...
уm	bm	lm1	lm2	...	lmn

1 етап. Пошук допустимого рішення.

Вільні змінні дорівнюють 0, а базисні дорівнюють відповідним вільним членам. Отже, якщо всі вільні члени ³ 0, то рішення – допустиме.

Якщо один з них < 0, то виконується заміна змінних.

2 етап. Пошук оптимального рішення.

Якщо всі коефіцієнти цільової функції будуть ³ 0, то виконується пошук оптимального рішення за допомогою заміни змінних.