Постановка основної задачі лінійного програмування (ОЗЛП).

Припустимо, що мають місце n змінних х₁, х₂,..., x_n. При цьому всі вони невід’ємні, тобто х₁³0, х₂³0,..., x_n³0. Також мають місце m умов - обмежень, які виражають за допомогою m рівнянь:

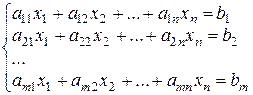(1)

Тобто, обмеження задані у вигляді рівнянь:

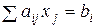
Цільова функція має вигляд:

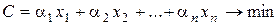
Умова задачі: знайти невід’ємні значення змінних х₁, х₂,..., x_n, які задовольняють системі рівнянь (1) і при яких цільова функція обертається в мінімум.

Якщо необхідно, щоб цільова функція оберталася в максимум, то треба змінити знак функції і розглянути функцію:

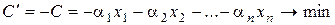
Допустиме рішення ОЗЛП – це деяка сукупність невід’ємних значень х₁, х₂,..., x_n, які задовольняють системі рівнянь (1).

Оптимальне рішення ОЗЛП – це те рішення з допустимих, при якому цільова функція обертається в мінімум.

ОЗЛП може і не мати рішень у таких випадках:

– якщо система (1) несумісна, тобто її рівняння суперечать одне одному;

– якщо є рішення системи, але серед х₁, х₂,..., x_n мають місце від’ємні значення;

– якщо є допустимі рішення, але цільова функція не обмежена знизу (немає оптимального рішення).

У випадку, коли n змінних дорівнює m рівнянням і рішення існує, то це рішення буде єдиним і оптимальним.

Основний випадок – коли n змінних більше m рівнянь.

З m рівнянь можна знайти значення тільки m змінних, які називають базисними. Решту n-m змінних називають вільними.

Якщо вільним змінним присвоїти деякі довільні значення, то решту - базисні змінні - можна однозначно визначити з m рівнянь. Така система має безліч рішень.

В окремих практичних задачах обмеження можуть задаватися нерівностями:

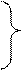
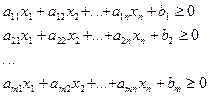(2)

В цьому випадку, треба систему нерівностей замінити системою рівнянь, тобто привести до ОЗЛП.

Якщо позначити 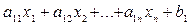як y₁, то отримаємо: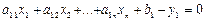

або 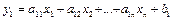(³0)

Тобто вводяться додаткові змінні y₁, y₂,...,y_m.

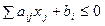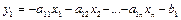Якщо нерівності мають вигляд , спочатку слід привести їх до вигляду , тобто (³0)

При приведенні до ОЗЛП:

m+n – загальна кількість змінних;

m – рівнянь Þ m базисних змінних;

(m+n)-m – кількість вільних змінних.