По результатам для дискретных факторов

Переменные факторы	Случайные факторы	Математическое ожидание целевой функции
		…		…
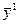
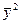
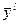
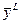
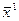
	p1 e11	p2 e12	…	pl e1l	…	pL e1L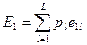
	p1 e21	p1 e22	…	pl e2l	…	p1 e2L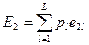
…	…	…	…	…	…		…
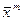
	p1 em1	p1 em2	…	pl eml	…	p1 emL
…	…	…	…	…	…	…	…
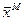
	p1 eM1	p1 eM1	…	pl eMl	…	p1 eM1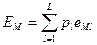

Набор значений переменных, при котором достигается максимальное (минимальное) значение математического ожидания, является оптимальным.

На практике способ осреднения по результату реализуют с помощью метода статистического моделирования. Обобщенный алгоритм этого метода следующий:

1. Для каждой из случайных величин y_k производят случайное испытание при соответствующем законе распределения с параметрами 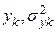и вычисляют ее значение.

2. Эта операция повторяется до тех пор, пока не будут найдены значения всех случайных величин .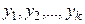

3. Используя найденные величины 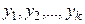, вычисляют частное значение e по заданной функции.

4. Операции 1. 2, 3 повторяют до тех пор, пока не будет получено N значений функции е.

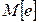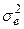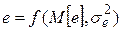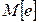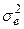На основании найденных значений e вычисляют плотность распределения вероятностей, а затем математическое ожидание и дисперсию случайной величины e. Эта величина может быть теперь записана в виде , где , задается как функция входных величин или параметров.

В связи с тем, что при статистическом моделировании математическая модель задана в виде моделирующего алгоритма, для поиска оптимальных решений обычно используют метод экспериментальной последовательной оптимизации на ЭВМ.

Способ осреднения по результату не ликвидирует влияния на результат фактора случайности. Результат каждого отдельного расчета, осуществляемого при случайных, заранее не известных значениях величин 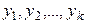, может сильно отличаться от ожидаемой средней как в лучшую, так и в худшую сторону, однако при многократном повторении расчетов эти различия в среднем сглаживаются. Чтобы составить представление о том, каков риск в каждом отдельном случае, желательно, кроме математического ожидания интересующего показателя, оценивать также и его дисперсию.

Метод статистического моделирования, реализующий способ осреднения по результату, основан на общих теоремах теории вероятностей, не содержит никаких ограничений и может быть применен к решению любой задачи, а при достаточно большом числе реализаций от него можно требовать любой точности. Указанные достоинства метода обусловили его широкое применение для решения самых сложных задач моделирования производственных процессов.

Вместе с тем метод статистического моделирования обладает и недостатком – большой трудоемкостью расчетов, поэтому стал широко применяться только с момента развития электронной вычислительной техники. Использование теории оптимального планирования экспериментов позволяет сокращать объемы расчетов без снижения точности за счет целенаправленного формирования статистических выборок.

Сокращению объема вычислений способствует также следующий прием. На первом этапе оптимизации используется способ искусственного сведения к детерминированной схеме; на втором – способ осреднения по результату, где начальным для проведения оптимизации является оптимальное решение предыдущего этапа.