Методы многокритериальной оптимизации
Эффективность функционирования производственных объектов любой сложности количественно оценивается соответствующими системами технико-экономических показателей. При этом очевидно, что оптимальное значение одного или нескольких показателей не означает, что данное состояние объекта наилучшее, так как значения остальных показателей для него могут быть ниже, чем для других состояний.
В этих условиях возникает задача нахождения такого состояния (например, варианта плана производства продукции), в котором значения всех рассматриваемых показателей были бы пусть и не оптимальными, но в определенном смысле наилучшими по выполнению всех показателей одновременно. Такие планы называют компромиссно-оптимальными, а задачи их поиска – принятием сложного решения.
С формальной точки зрения назначение каждого объекта (или его отдельного элемента) состоит в том, чтобы преобразовать входные сигналы в выходные. Описательная математическая модель для любого объекта могла бы представлять систему соотношений вида
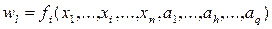 , (3.11)
, (3.11)
где wl – выходные характеристики объекта; 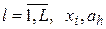 – факторы, на базе которых строится модель объекта (параметры, характеристики окружения, начальные условия, время);
– факторы, на базе которых строится модель объекта (параметры, характеристики окружения, начальные условия, время); 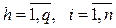 .
.
Однако на практике получение адекватной исследуемому явлению модели такого вида, когда характеристики процесса являются явными функциями от входных факторов, бывает достаточно редко. В общем случае для сложных производственно-экономических систем эта задача может оказаться непосильной, что существенно сужает область использования "классических" методов исследования экономических операций (линейное, нелинейное и динамическое программирование, теория массового обслуживания, задача управления запасами, ремонта и замены оборудования и др.). Поэтому для описания и исследования таких объектов в последнее время стало интенсивно развиваться новое направление – имитационное моделирование.
В самом общем виде многокритериальная оптимизационная математическая модель представляется соотношениями
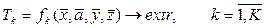 ; (3.12)
; (3.12)
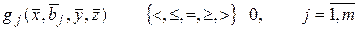 . (3.13)
. (3.13)
В оптимизационной математической модели, определяемой выражениями (3.12) и (3.13), выходные факторы объекта wl модели (3.11) в записи не отражены, хотя, естественно, и критерий, и ряд ограничений определяются через эти характеристики. Множество входных факторов модели 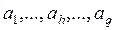 и входных факторов ее отдельных модулей в записи модели (3.12)-(3.13) подразделяется на переменные объекта
и входных факторов ее отдельных модулей в записи модели (3.12)-(3.13) подразделяется на переменные объекта 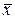 , константы
, константы 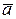 и
и 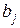 , случайные
, случайные 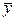 и неопределенные
и неопределенные 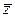 факторы.
факторы.
К общей формулировке многокритериальной задачи принятия решения могут сводиться задачи различного происхождения, которые можно классифицировать по четырем типам:
1. Задачи оптимизации на множестве целей. Имеется множество разнородных целей, каждая из которых должна быть учтена при выборе оптимального решения.
2. Задачи оптимизации на множестве объектов. Рассматривается совокупность объектов, качество функционирования каждого из которых оценивается самостоятельным критерием; качество функционирования совокупности объектов оценивается векторным критерием, составленным из частных критериев, характеризующих каждый объект.
3. Задачи оптимизации на множестве условий функционирования – задан спектр условий, в которых предстоит работать объекту, и применительно к каждому условию качество функционирования оценивается некоторым частным критерием.
4. Задачи оптимизации на множестве этапов функционирования – рассматривается функционирование объекта на некотором интервале времени, разбитом на несколько этапов; качество управления на каждом этапе оценивается частным критерием, а на множестве этапов – общим векторным критерием.
В задачах 2, 3, 4-го типа частные критерии имеют обычно единую размерность.
Для случая, описываемого выражениями (3.12), (3.13), вид платежной матрицы (см. табл. 3.2) остается прежним. Платежные матрицы, соответствующие каждому частному критерию, будут образовывать макростолбцы общей платежной матрицы исследуемой ситуации. Для случая детерминированной задачи вся информация для принятия решения также будет соответствовать определенному критерию, а не набору значений неопределенных факторов.
Наиболее сложным для практики является решение задач первого типа, для которых множество критериев оптимальности в принципе не имеет единой размерности. Для возможности сравнения частных решений необходимо приведение частных критериев к одинаковой размерности. Наиболее распространенным способом решения этой проблемы является нормировка критериев – приведение их к безразмерному виду по формулам
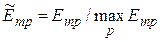
для критериев, которые стремятся увеличивать, и
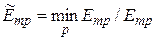
для критериев, которые стремятся уменьшить. При этом 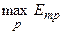 и
и 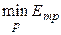 означают соответственно максимальное или минимальное значение p-го критерия оптимальности.
означают соответственно максимальное или минимальное значение p-го критерия оптимальности.
Таким образом, после нормировки вместо матрицы 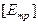 , в которой элементы столбцов имели различную размерность, получается матрица
, в которой элементы столбцов имели различную размерность, получается матрица 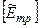 , размерность элементов которой от 0 до 1:
, размерность элементов которой от 0 до 1: 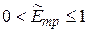 .
.
К полученной матрице 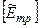 в принципе можно применять критерии, приведенные выше. Однако в ситуации принятия решений по многим критериям исследователь зачастую обладает дополнительной информацией о важности того или иного критерия оптимальности. Эта эвристическая информация с помощью методов экспертной оценки может формироваться в виде коэффициентов важности каждого p-го критерия –
в принципе можно применять критерии, приведенные выше. Однако в ситуации принятия решений по многим критериям исследователь зачастую обладает дополнительной информацией о важности того или иного критерия оптимальности. Эта эвристическая информация с помощью методов экспертной оценки может формироваться в виде коэффициентов важности каждого p-го критерия – 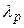 .
.
В литературе описываются всевозможные принципы оптимальности и соответствующие им схемы компромисса между решениями, получаемыми по частным критериям. Сюда относятся принципы равенства, квазиравенства, равномерности, справедливой абсолютной и относительной уступки, последовательной уступки, выделения главного критерия и ряд других. До недавнего времени наиболее часто использовались следующие показатели свертки нескольких критериев оптимальности в единую целевую функцию:
критерий справедливости абсолютной уступки
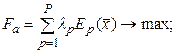
критерий справедливости относительной уступки
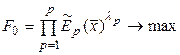 ,
,
где 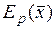 – нормированное значение p-го критерия оптимальности
– нормированное значение p-го критерия оптимальности 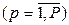 ; λp – коэффициент важности свертки p-го критерия.
; λp – коэффициент важности свертки p-го критерия.
Однако, как показала практика, в большинстве случаев оптимальное решение достаточно чувствительно к изменению коэффициентов важности λp. Получение этих коэффициентов экспертными методами дает достаточно большую величину доверительного интервала для их средних значений. Даже незначительная область изменения значений коэффициентов важности приводит к появлению множества решений, оптимальных для этой области, – к "размыванию" оптимального решения.
Именно поэтому в последнее время большое распространение среди методов многокритериальной оптимизации получили человекомашинные процедуры. В отличие от других групп методов многокритериальной оптимизации, где мнение руководителя (в дальнейшем лица, принимающего решение, или сокращенно ЛПР) о важности отдельных критериев в том или ином виде выявляется до решения конкретной задачи, человекомашинные процедуры работают в диалоговом (интерактивном) режиме с ЛПР. Машинная программа, реализующая человекомашинную процедуру, выводит информацию для ЛПР в виде распечаток или непосредственно на дисплей. ЛПР анализирует эту информацию и вырабатывает свои представления по поводу соотношения важности целей в конкурентной ситуации, в том числе и с учетом качественной, неформализуемой информации, затем эти новые предпочтения вводятся в ЭВМ и происходит их обработка. Далее для ЛПР вновь выводится информация, в которой учтено его предыдущее мнение, и цикл повторяется до тех пор, пока не будет получено решение, удовлетворяющее ЛПР. Различные человекомашинные процедуры отличаются друг от друга видом информации, представляемой ЛПР на каждой итерации, а также формой, в которой ЛПР вырабатывает и вводит в ЭВМ предпочтения по важности целей. Выбор той или иной процедуры для решения конкретной задачи должен основываться на максимально полном удовлетворении следующих требований: обеспечение доверия ЛПРом; пригодность получаемой информации для принятия решения; высокая скорость сходимости решения.
Максимальное доверие к решению обеспечивают процедуры, в которых удается наиболее наглядно показать все альтернативные решения, обеспечить легкость использования и понимания метода работы человекомашинной процедуры ЛПР, сходство действий ЛПР с методикой его работы без использования процедуры. Иллюстрацией работы человекомашинной процедуры может быть пример использования модифицированной процедуры С. Зайонца и Ю. Валлениуса.
Укрупненный алгоритм модифицированной процедуры следующий.
1. Ввод исходной информации для расчета значений критериев 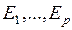 и ограничений математической модели.
и ограничений математической модели.
2. Присвоение начальных значений коэффициентам важности для свертки критериев оптимальности в единую целевую функцию вида 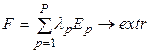 (max и min в зависимости от смысла решаемой задачи). При этом должно выполняться условие
(max и min в зависимости от смысла решаемой задачи). При этом должно выполняться условие 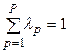 . Для первой итерации допустимо задавать равные значения коэффициентов
. Для первой итерации допустимо задавать равные значения коэффициентов 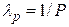 .
.
3. Решение задачи отыскания оптимального (базового) решения модели на основе единой целевой функции
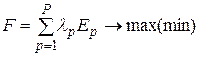 . (3.14)
. (3.14)
4. Генерация близких к базовому вариантов свертки критериев, которые получаются за счет последовательного увеличения каждого из коэффициентов важности в соответствии с отклонениями е.
Например, при наличии трех критериев оптимальности возможно формирование трех вариантов ( 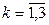 ), близких к базовому по критериям
), близких к базовому по критериям
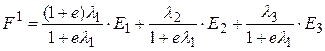 ,
,
если предполагается увеличение на величину е первого критерия;
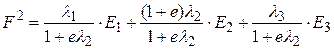 ,
,
если увеличивается второй критерий, и
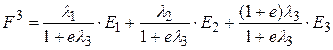
при увеличении третьего критерия.
5. Решение задач отыскания оптимального решения для всех сгенерированных вариантов, близких к базовому, по вновь полученным в п. 4 целевым функциям и вывод на печать или дисплей базового или близких к нему вариантов решений.
6. Анализ базового или близких к нему вариантов решения ЛПР и ввод парных предпочтений для каждого из вариантов решений по отношению к базовому ("+" – вариант более предпочтителен, чем базовое решение; "-" – вариант менее предпочтителен, чем базовое решение).
7. Если нет положительных предпочтений по вариантам решений, то вывод на печать значений критериев и переменных, которые являются оптимальными, и окончание работы процедуры.
8. Если есть положительные предпочтения по вариантам решений, формируются целевая функция и ограничения для решения вспомогательной задачи корректировки значений коэффициентов важности свертки критериев ( 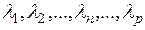 ) для следующей итерации поиска базового варианта. Целевая функция
) для следующей итерации поиска базового варианта. Целевая функция
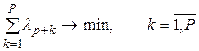 . (3.15)
. (3.15)
При этом ограничения при максимизации единой целевой функции имеют вид:
а) для каждого k-го варианта, который признан ЛПР более предпочтительным, чем базовый,
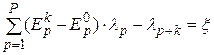 , (3.16)
, (3.16)
где ξ – некое достаточно малое число, например, ξ = 0,001; 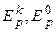 – значение p-го критерия для k-го и базового вариантов соответственно;
– значение p-го критерия для k-го и базового вариантов соответственно;
б) для каждого k-го варианта, который признан ЛПР менее предпочтительным, чем базовый, записываются ограничения вида
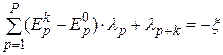 ; (3.17)
; (3.17)
в) получившийся набор значений 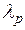 должен соответствовать условию
должен соответствовать условию
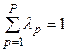 . (3.18)
. (3.18)
9. Получение новых значений коэффициентов свертки критериев ( 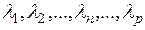 ) при решении математической модели (3.15) – (3.18) с помощью симплекс-метода и переход к блоку 3.
) при решении математической модели (3.15) – (3.18) с помощью симплекс-метода и переход к блоку 3.
При минимизации единой целевой функции (3.14) ограничения (3.16) и (3.17) меняются местами.
В заключение отметим, что на этапе решения математической модели к ранее описанным ограничениям и допущениям могут добавляться допущения и ограничения, принятые при использовании полученной математической модели (например, ограничения, налагаемые используемой вычислительной техникой, упрощения исходной математической модели для возможности применения аналитических методов и др.).
Дата добавления: 2015-12-16; просмотров: 1493;
