Экспериментальная оптимизация на ЭВМ

Если математическая модель непригодна для применения аналитических или численных методов, а это присуще всем моделям алгоритмического вида, то для ее решения применяют метод экспериментальной оптимизации ЭВМ. При этом методе не обязательно преобразовывать математическую модель в специальную систему уравнений.

Как целевая функция, так и система ограничений могут быть заданы в виде алгоритма, позволяющего вычислить их значения в ходе моделирования. Как уже указывалось выше, характерным примером алгоритмических моделей являются имитационные модели, реализуемые на ЭВМ в виде моделирующего алгоритма.

В процессе реализации данного метода, так же как и для любого численного метода, выполняются перечисленные выше этапы: выбор начальных значений переменных, расчет значения целевой функции, определение направления и шага изменения переменных и т.д., в связи с чем он является численным методом, имеющим своеобразные отличия.

Каждый численный метод нахождения оптимальных решений в задачах математического программирования ориентирован на какой-то класс математических уравнений, для которого он является либо единственным методом решения, либо наиболее эффективным. В рамках данного метода обоснованы и выбор начальных значений переменных, и вопросы анализа получения результатов с целью определения направления и шага их изменения.

Алгоритмические модели в силу специфичности их математической записи не позволяют в ряде случаев даже качественно определить вид целевой функции (например, мономодальная или полимодальная). В связи с этим перед исследователем, помимо создания моделирующего алгоритма, возникают проблемы разработки алгоритма оптимизации, включающего моделирующий алгоритм в качестве одного из элементов – этапа расчета значения целевой функции для определенных значений переменных. Для этого им должна быть продумана алгоритмическая и программная реализация всех вышеназванных этапов.

Существуют два метода экспериментального поиска оптимальных решений: параллельный и последовательный. При использовании параллельного метода все комбинации значений переменных, при которых должны рассчитываться значения целевой функции, выбираются заранее, в то время как в случае применения последовательного метода заранее определяется несколько начальных значений, а остальные выбираются лишь по мере накопления данных.

Два основных параллельных метода называются методами случайного поиска и многофакторного анализа, они основаны на априорном выборе определенных интервалов изменения переменных x₁, x₂,.., x_n. Границы этих интервалов определяются, с одной стороны, из предположения, что внутри них находятся оптимальные значения 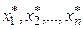, а с другой – из условия выполнения ограниченной модели.

В первом методе случайным образом устанавливаются точки эксперимента, в которых значения x₁, x₂,.., x_n принадлежат этим интервалам, причем выбор значения каждой переменной производится независимо. Для каждой зафиксированной точки рассчитывается значение целевой функции. В качестве решения выбирается такая точка, для которой целевая функция принимает экстремальное значение, либо производится более тщательный поиск экстремума в окрестности этой точки (обычно методом многофакторного анализа).

При использовании метода многофакторного анализа интервалы изменения каждой из n переменных разбиваются на m подинтервалов, которые определяют уровни их изменения. Значения переменных для точек эксперимента формируют путем объединения значений по каждому уровню для всех переменных, что дает в результате N экспериментов (полный факторный эксперимент):

,

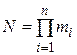где m_i – число значений (уровней), i = 1, 2, .., n – число переменных модели.

Далее для каждой точки рассчитывается значение целевой функции и либо выбирается наилучшая точка, либо более тщательно (т.е. с меньшей величиной подинтервалов) исследуется окрестность этой точки. Различия между описанными параллельными методами экспериментальной оптимизации показаны на рис. 3.7.

Рис. 3.7. Параллельные методы экспериментальной оптимизации на ЭВМ

Последовательные методы экспериментального поиска чаще всего основаны на принципах построения численных методов, описанных выше. В качестве базовых используются симплекс-метод, метод покоординатной оптимизации, градиентный метод и его модификация.

Однако далеко не всегда возможно проведение последовательного экспериментального поиска на принципах численного метода. Трудности строгой математической формализации и разработки методов нахождения оптимальных решений в задачах проектирования сложных систем или процессов и управления ими привели к созданию большого числа так называемых эвристических алгоритмов поиска наилучших решений для решения разнообразных практических задач. Примерами подобных алгоритмов служат многочисленные методы решения задач оперативно-календарного планирования производства, каждый из которых формализует опыт специалистов при формировании планов запуска-выпуска деталей в тех или иных специфических условиях. С содержательной точки зрения эвристические алгоритмы представляют собой набор правил конструирования, сравнения, анализа и отбора вариантов возможных решений. От алгоритмов математического программирования эти алгоритмы отличаются тем, что они не гарантируют получение оптимального решения – в них производится выбор наилучшего решения из просмотренных.

Качество эвристических алгоритмов зависит от того, насколько тесно связаны правила отбора вариантов, лежащих в основе этих алгоритмов, с "идеальными" правилами отбора, вытекающими из точной постановки задачи. Эвристические алгоритмы обычно применяются для проектирования и управления объектами с большим набором признаков и свойств, для которых, с одной стороны, затруднительно полное математическое описание и применение разработанного математического аппарата, а с другой – возможно построить достаточно простые и гибкие правила отбора вариантов.

При использовании любого метода последовательной экспериментальной оптимизации на ЭВМ все работы по алгоритмизации, программированию и отладке модели приходится выполнять разработчику модели. От правильности выбора исследователем принципов построения алгоритма последовательной экспериментальной оптимизации во многом зависят объемы вычислений при нахождении оптимального решения.

3.8.2. Поиск решений при наличии в модели случайных
и неопределенных факторов

Для того чтобы задача поиска оптимального решения могла быть классифицирована как задача принятия решения в условиях риска, необходимо, чтобы все случайные факторы были для исследования статистически полностью определены, т.е. для k-го случайного фактора y_k должен быть известен закон распределения вероятностей появления его отдельных значений p(y_k).

Значение целевой функции стохастической модели зависит от управляемых переменных, констант и значений случайных факторов, поэтому результаты моделирования, полученные при воспроизведении единственной реализации, не могут объективно характеризовать изучаемый объект:

;

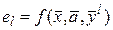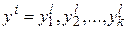, (3.6)

где e_l – случайное значение целевой функции для l-й реализации случайных факторов.

В связи с этим при нахождении оптимальных значений переменных стохастическую задачу принятия решений сводят к детерминированной одним из двух принципиально различных способов: искусственное сведение к детерминированной модели; осреднение по результату.

В первом случае вероятностная картина явления приближенно заменяется детерминированной: вместо законов распределения все включенные в модель случайные факторы заменяются их математическими ожиданиями, в результате чего стохастическая модель переходит в детерминированную. Этот способ всегда используется при переводе случайных факторов в детерминированные на этапе выбора существенных факторов модели.

Во всех ли случаях правомерна такая замена? Ответить на этот вопрос можно простейшим примером. Пусть результат функционирования системы e зависит от закона распределения случайной величины y. Проверим, будет ли выполняться равенство

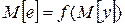. (3.7)

а) Линейная функция e = a+by

.

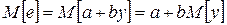Равенство (3.7) справедливо.

b) Нелинейная функция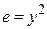

,

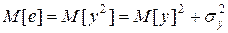т.е. равенство (3.7) несправедливо. Имеется смещение математического ожидания целевой функции на величину 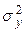. Таким образом, допущение о возможной замене случайных величин их математическими ожиданиями в общем случае неверно.

Искусственное сведение к детерминированной модели не приводит к погрешностям в расчетах математического ожидания результата только в тех случаях, когда целевая функция и ограничения зависят от случайных факторов линейно.

Нелинейность математической модели приводит к возникновению погрешностей расчета тем больше, чем больше нелинейность. Поэтому этот способ применяется преимущественно в грубых, ориентировочных расчетах, а также в тех случаях, когда диапазон возможных значений случайных величин сравнительно мал, т.е. они без большой натяжки могут рассматриваться как неслучайные величины. Основанием для его использования может служить значение коэффициента вариации случайной величины, определяемой как

,

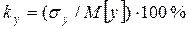где 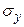– среднее квадратическое отклонение случайного фактора y;
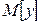– математическое ожидание случайного фактора y.

Если коэффициент вариации менее 15-20%, то замена случайного фактора его математическим ожиданием обычно не приводит к существенным погрешностям.

После сведения стохастической модели к детерминированной для поиска оптимальных решений используются аналитические, численные и экспериментальные методы поиска экстремума. Выбор того или иного метода определяется свойствами преобразованной к детерминированному виду математической модели.

Способ осреднения по результату более сложен и применяется в тех случаях, когда разброс случайных факторов велик и замена каждого из них его математическим ожиданием может привести к большим ошибкам. Он состоит в замене случайной целевой функции (3.6) ее статистической характеристикой – математическим ожиданием

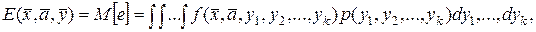(3.8)

где p(y₁, .., y_k) – многомерный закон распределения случайной величины .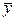

При оптимизации по целевой функции (3.8) выбираются такие значения 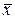, которые приводят к максимизации (минимизации) математического ожидания:

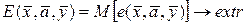. (3.9)

При этом, естественно, выполняются все ограничения математической модели.

В связи с тем, что результат, полученный при воспроизведении единственной реализации, не может характеризовать воспроизводимый процесс в целом, приходится анализировать большое число таких реализаций. Только тогда по закону больших чисел получаемые оценки приобретают статистическую устойчивость и могут быть приняты с достаточной точностью за оценки искомых величин.

Аналогом выражения (3.8) для дискретных факторов служит выражение

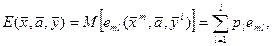(3.10)

где 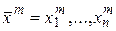– m-й набор значений переменных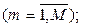 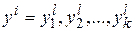– l-й набор значений случайных факторов 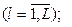p_l – вероятность появления l-го набора случайных факторов;
е_ml – значение целевой функции при m-м наборе значений переменных и l-м наборе значений случайных факторов.

Исходная информация о подобной ситуации заносится в таблицу (табл. 3.1); в последней графе каждой строки записываются результаты расчета математического ожидания целевой функции.

Таблица 3.1