Построение эпюр в рамах

Рама представляет собой систему прямых стержней, определенным образом соединенных между собой.

В простейшем случае рамой может быть балка с ломаным очертанием оси. Вертикальный элемент рамы называется стойкой, горизонтальный – ригелем. Рамы бывают плоскими и пространственными Примером плоской рамы является поперечник промышленного здания. В отличие от балки на раму кроме вертикальных нагрузок действуют и горизонтальные нагрузки. Порядок определения реакций в раме практически не отличается от балок. Рассмотрим алгоритм определения реакций в раме на следующем примере.

Пример 8.5. Определить опорные реакции в раме, изображенной на рис.8.14.

1. ΣF_z = 0. H_A – P = 0 → H_A = P = 2 кН

2. Σm_A = 0. – M + P·6 + q·4·4 + P·3 – B·6 = 0 → B = 10 кН

3. Σm_B = 0. – M – q·4·2 + P·3 + A·6 = 0 → A = 4 кН

4. ΣF_y = A – q·4 – P + B = 4 – 12 – 2 + 10 = 14 – 14 = 0

Реакции найдены верно.

Порядок построения эпюр M_x, Q_y, N_z в рамах такой же, как и балках. Эпюра изгибающих моментов строится со стороны растянутых волокон балки. Положение растянутого волокна определяется аналитически в соответствии с уравнением М_х.

Правило знаков для поперечной силы в рамах такое же, как и балках. В рамах, помимо названных внутренних усилий, действует еще и продольная сила, которая определяется методом сечений. Порядок построения эпюр рассмотрим на примере 8.6.

Пример 8.6. Построить эпюры M_x, Q_y, N_z для рамы, изображенной на рис. 8.15

1. ΣF_z = 0. H_A – P = 0 → H_A = P = 2 кН

2. Σm_A = 0. – M + P·4 + q·4·2 + P·3 – B·4 = 0 → B = 6 кН

3. Σm_B = 0. – M – q·4·2 + P·1 + A·4 = 0 → A = 6 кН

4. ΣF_y = A – q·4 + B = 6 – 12 – 6 = 12 – 12 = 0

Реакции найдены верно.

Рама имеет четыре участка. На каждом участке рамы проводим сечение и рассмотрим в равновесии одну из частей рамы. Правую или левую, верхнюю или нижнюю.

1. Участок AD

0 ≤ z ≤ 3

Q_y = H_A = 2 кН

M_x = – H_A·z₁·M₀ = 0, М₃ = – 6 кНм

ΣF_z = 0 A + N₁ = 0 → N = – A = – 6 кН

Уравнение моментов записано для случая, когда наблюдатель находится слева от стойки AD . Эпюра М_х отрицательная, поэтому откладывается справа от стойки AD . Когда наблюдатель находится слева от AD , знак изгибающего момента меняется. Теперь ординаты эпюры моментов откладываются, как и в предыдущем случае, справа от стойки AD . По этой причине в рамах на эпюрах изгибающих моментов знак не ставится.

2. Участок СD

0 ≤ z₂ ≤ 2

Q_y = 0

M_x = – M = – 8 кНм

ΣF_z = 0 → N₂ = 0

3. Участок DE

0 ≤ z₃ ≤ 1

Q_y = P = 2 кН

M_x = – P·z₃, M₀ = 0, M₁ = 2 кНм,

ΣF_z = 0 → N₃ = 0

4. Участок ВD

0 ≤ z₄ ≤ 4

Q_y = B + q·z·Q₀ = – 6 кН, Q₄ = – 6 + 12 = 6 кН

M_x = –B·z₄ – · M₀ = 0, М₄ = 0, 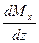= B - q·z = 0, z = = 2 мм

M_max = B·2 – 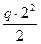= 12 – 6 = 6 кНм, N₄ = 0

По найденным значениям M_x, Q_y, N_z строим соответствующие эпюры (рис 8.16)

Следовательно, узел D находится в равновесии.