Геометрическое построение изображений

Изображения могут быть построены при помощи простых правил оптики и геометрии.

Как можно увидеть из рис. 3.11, для построения изображения объекта требуется, как минимум, два луча.

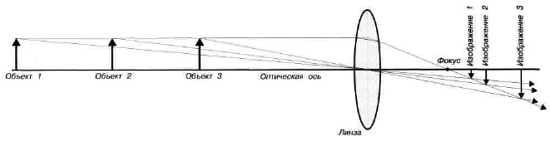
Рис. 3.11. Проекции изображений объектов, находящихся на различных расстояниях

При построении изображений следует придерживаться следующих трех правил:

• Объекты, находящиеся на различных расстояниях, на схеме должны одним концом касаться оптической оси.

• По определению, лучи, проходящие через центр линзы, не меняют своего направления, т. е. в центре линза ведет себя как плоскопараллельная стеклянная пластина, не вызывая преломления.

• По определению, лучи, параллельные оптической оси, проходят через фокус.

Вспомним теперь основную формулу линзы, которую мы используем при расчете количества света, падающего на ПЗС‑матрицу:

1/D + 1/d = 1/f (30)

здесь D – расстояние от объекта до линзы, d – расстояние от линзы до изображения f – фокусное расстояние линзы.

Отметим, чтоd здесь относится к изображению не бесконечно удаленного объекта, и поэтому оно больше, чем 1; а в случае бесконечно удаленного объекта d будет равно 1.

Обратите, пожалуйста, внимание на изображения объектов, находящихся на различном расстоянии. Фокусировка линзы достигается за счет изменения расстояния между линзой и плоскостью изображения (где расположена ПЗС‑матрица). Итак, проекция изображения совпадает с фокальной плоскостью только в том случае, когда линза сфокусирована на бесконечно удаленный объект. Во всех остальных случаях расстояние между линзой и изображением больше, чем фокусное расстояние линзы.

Следует также отметить, что (как упоминалось выше) на практике объектив состоит из нескольких оптических элементов. Следовательно, их можно представить эквивалентной одноэлементной линзой, расположенной в главной точке. Рис. 3.13 поясняет этот момент.

Объектив, образованный из нескольких оптических элементов (единичных тонких линз), имеет две главных точки – первую и вторую главные точки. Для тонкой линзы эти точки совпадают и расположены в центре линзы.

Плоскости, пересекающие эти главные точки и перпендикулярные оптической оси, называются главными плоскостями.

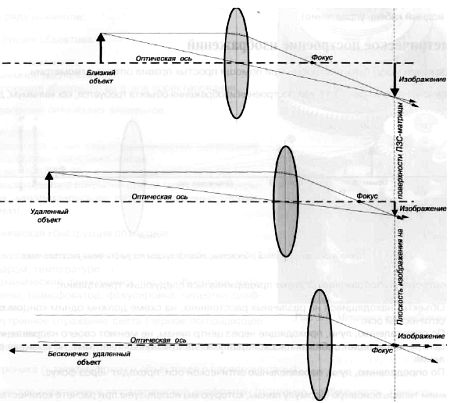
Рис. 3.12. Концепция фокусировки

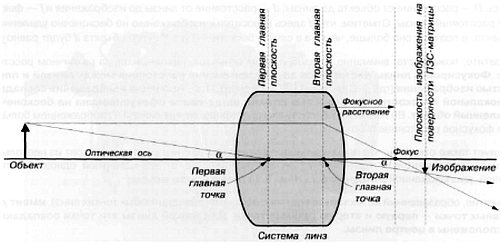
Рис. 3.13. Основные точки и плоскости

Главные плоскости обладают следующими свойствами:

• Луч, падающий на первую главную плоскость (параллельно оптической оси), покинет вторую главную плоскость на той же высоте, распространяясь в направлении точки фокуса.

• Луч, падающий в направлении первой главной точки, покинет вторую главную точку под тем же углом.

• Фокусное расстояние такой линзы принимается равным расстоянию от второй главной плоскости до фокуса.

Пользуясь этими свойствами, можно построить геометрическое изображение таким же образом, как в случае линзы, состоящей из одного оптического элемента.

Следует отметить, что вторая главная точка может попасть за объективов с маленьким фокусным расстоянием. Чем меньше пределы системы линз – в случае фокусное расстояние, тем больше оптических элементов необходимо добавлять для коррекции различных искажений, что увеличивает стоимость объектива. С уменьшением формата ПЗС‑матриц (от 2/3" до 1/2" и 1/3", a теперь и до 1/4". В настоящее время выпускаются телекамеры с ПЗС‑матрицами 1/6".Прим. ред .) приходится производить объективы с более коротким фокусным расстоянием, чтобы сохранить тот же по ширине угол зрения.

Это, в свою очередь, вынудило промышленность уменьшить расстояние от фланца объектива до плоскости изображения, которое для «С» типа крепления равно 17.5 мм с тем, чтобы оптика стала проще, меньше, дешевле.

Новый формат расстояния равен 12.5 мм, и поскольку он меньше, он называется стандартом CS (S‑small).

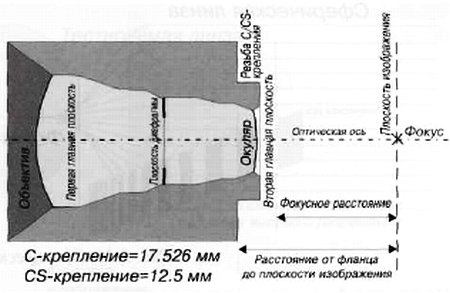
Рис. 3.14. Поперечное сечение объектива с ручной установкой диафрагмы

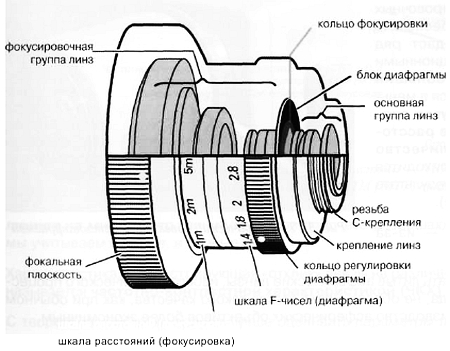
Рис. 3.15. Поперечное сечение объектива с ручной установкой диафрагмы

Асферические линзы

Как уже упоминалось выше, сферическая аберрация – это общий тип искажения, присущий большинству линз сферического типа. Линзы сферического типа наиболее распространены, поскольку изготавливаются они при помощи самых простых механических способов шлифовки и полировки, подчиняющихся сферическим законам. Полировка выполняется круговой машиной, в результате чего линза имеет сферическую форму. Можно показать, что кроме хроматической аберрации, присущей простому оптическому элементу («разложение на цвета» белого света), есть еще и сферическая аберрация, вызванная сферическим профилем линзы. Фокус не является в точности одной точкой.

На основе физических законов преломления можно показать (но мы не будем вдаваться в эти детали), что колоколоподобная линза (не сферическая) является идеальной для получения единой фокусной точки без сферических искажений. Поперечное сечение такой линзы представляет собой кривую, несколько отклоняющуюся от формы окружности и имеющую форму колокола.

Это продемонстрировано на рис. 3.16, и чтобы было понятнее – в преувеличенной форме. Такая линза называется асферической.

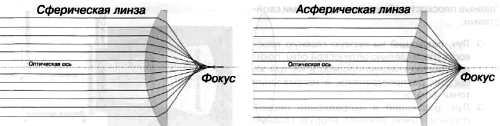
Рис. 3.16. Сферическая и асферическая линзы

Понятно, что такую форму трудно воспроизвести при помощи стандартных полировочных технологий, но, если все‑таки обеспечить качественное изготовление, она даст ряд преимуществ в сравнении с традиционными сферическими линзами, включая больший раскрыв диафрагмы (что отражается в меньших значениях F‑числа), больший угол зрения, более короткое минимальное расстояние до объекта, меньшее количество оптических элементов, так как приходится исправлять меньше аберраций (в результате объектив становится меньше и легче).

Однако такая технология дороже – из‑за сложной техники полировки.

Оптические компании начали выпускать литые асферические линзы, избегая критического процесса шлифования. Этот процесс, правда, не обеспечивает стекла такого качества, как при обычном процессе, но позволяет сделать производство асферических объективов более экономичным.

Качество таких объективов еще нуждается в доказательствах, но они существуют и доступны на рынке оборудования для систем видеонаблюдения.

Рис. 3.17. Асферический объектив с автодиафрагмой