Касательные напряжения в балке двутаврового поперечного сечения
 |
Особенностью двутаврового поперечного сечения является резкое изменение ширины сечения в месте перехода стенки двутавра к его полке (рис. 8.24). Поперечную силу в сечении воспринимает стенка двутавра, полка воспринимает небольшую часть поперечной силы.
Определим касательные напряжения в произвольной точке К. Для этого вычислим статический момент площади верхней заштрихованной части поперечного сечения
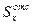= F1·y1 + F2·y2.
Этой формулой можно пользоваться тогда, когда точка К находится в пределах стенки двутавра
.
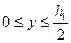Как было отмечено выше, формулой Журавского для определения касательных напряжений в полке пользоваться нельзя, так как ширина полки значительно больше ее высоты. Эпюра касательных напряжений в вертикальной стенке имеет вид, показанный на рис. 8.24.
В каждой точке двутавра возникают два касательных напряжения τx и τy. Учитывая, что для полки b>>hп, предположение о равномерном распределении касательных напряжений τy по ширине полки не выполняется. Однако касательные напряжения τy в полке не велики и практически не влияют на прочность балки. Поэтому ими, как правило, не интересуются и не вычисляют их значения.
При определении касательных напряжений τx будем полагать, что они по толщине полки распределяются равномерно. В этом случае для их определения можно воспользоваться формулой Журавского (рис. 8.25).
 |
Статический момент отсеченной площади определим по формуле:
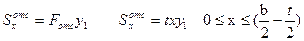
Дата добавления: 2015-12-11; просмотров: 1613;