МОДУЛЬ 5. ТЕОРИИ ПРОЧНОСТИ

Достаточно просто решается вопрос о прочности материала в точке тела, находящейся в условиях одноосного напряженного состояния (простого растяжения-сжатия). В этом случае в поперечном сечении действует только одно главное напряжение равное расчетному напряжению. Как известно условие прочности материала по несущей способности в этом случае записывается так:

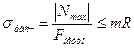, (5.1)

где R – расчетное сопротивление материала элемента конструкции. Формула (5.1) не может быть применена в условиях сложного напряженного состояния, когда в точке тела действуют более одного главного напряжения, оказывающие определенное влияние на прочность материала в этой точке. В формуле (5.1) фигурирует расчетное сопротивление материала R, определяемое из опыта на простое растяжение (сжатие) цилиндрических образцов. Подобную величину получить при сложном напряженном состоянии не представляется возможным. Для этого потребовалось бы проведения огромного числа испытаний материалов при различных сочетаниях главных напряжений. Поэтому на практике пользуются так называемыми гипотезами, или теориями прочности, где предполагается, что расчетное сопротивление R не зависит от вида напряженного состояния и может быть определено из опыта на простое растяжение (сжатие) цилиндрических образцов материала, из которого выполняется элемент конструкции.

Рассмотрим основные классические гипотезы прочности материалов в последовательности их создания.

5.1. Первая теория прочности. Теория наибольших нормальных напряжений – теория Галилея

Первая теория прочности основана на соображении о том, что два элемента конструкции, выполненные из одного и того же материала при разных видах напряженного состояния, равнопрочные, если равны между собой их наибольшие нормальные напряжения:

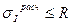(5.2)

В формуле (5.2) расчетное максимальное напряжение при плоском напряженном состоянии определяется по формуле (4.21). С учетом этого можем записать

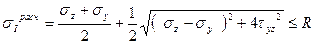(5.3)

При опытной проверке указанной гипотезы обнаружилось несоответствие с результатами опытов при испытаниях на всестороннее сжатие. Лишь для случая растяжения хрупких материалов эта теория согласуется с опытами. Так как эта теория дает либо излишние, либо недостаточные размеры элементов конструкций, работающих при сложном напряженном состоянии, она не нашла практическое применение.

5.2. Вторая теория прочности. Теория наибольших относительных деформаций – теория Мариотта

Вторая теория прочности пытается связать хрупкое разрушение не с величиной нормальных наибольших напряжений, а с величиной наибольшего относительного удлинения.

Эта теория основана на соображении о том, что два элемента конструкции, выполненные из одного и того же материала при разных видах напряженного состояния, равнопрочные, если равны между собой их наибольшие относительные деформации (удлинения).

Наибольшее относительное удлинение ε₁ при объемном напряженном состоянии (4.36)

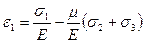, (5.4)

а при линейном напряженном состоянии относительное удлинение, при котором наступает опасное состояние, будет тогда, когда:

.

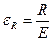Отсюда, согласно этой теории прочности, условие прочности принимает вид:

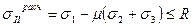(5.5)

Приведенные теории прочности страдают крупными недостатками. В одних случаях большую погрешность дает первая теория прочности, а в других случаях – вторая. Поэтому иногда II теория прочности применяются при расчете элементов конструкций, выполненных из хрупких материалов.

5.3. Третья теория прочности. Теория наибольших касательных напряжений – Сен-Венан, Кулон

В соответствии с третьей теорией прочности два элемента конструкции, выполненные из одного и того же материала, при различных напряженных состояниях будут равнопрочными, если равны их наибольшие касательные напряжения.

Наибольшие касательные напряжения при объемном напряженном состоянии определяются по третьей формуле (4.30), а при линейном напряженном состоянии наибольшие касательные напряжения, при которых наступает опасное состояние будет тогда, когда:

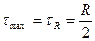(5.6)

Приравнивая (4.30) к (5.6), получаем:

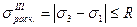(5.7)

В случае плоского напряженного состояния главные напряжения определяются по формуле (4.21).Тогда условие прочности согласно третьей теории принимает вид:

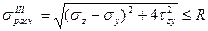(5.8)

В частном случае, когда σ_z=σ; τ_zy=τ; σ_y=0, формулу (5.8) перепишем так:

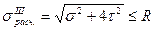(5.9)

Теория наибольших касательных напряжений достаточно близко подтверждается результатами опыта, особенно для пластичных материалов. Она также согласуется с результатами опытов при всестороннем сжатии. Размеры сечения элемента конструкции, найденные по этой теории, оказываются несколько завышенными.

Недостатком этой теории прочности является то, что она не учитывает влияние на прочность элемента конструкции, промежуточного по величине главного напряжения. Получается, что промежуточное главное напряжение σ₂ при условии, что σ₁ ≥ σ₂ ≥ σ₃ можно задавать произвольно. Этой теорией прочности недооценивается опасность разрушения элемента конструкции при действии примерно равных по величине главных растягивающих напряжений.

Поэтому возникла необходимость использовать новые подходы при оценке прочности элементов конструкций, находящихся в условиях сложного напряженного состояния.

5.4. Четвертая теория прочности – энергетическая

В основу энергетической теории прочности было вначале высказано положение о том, что причиной опасного состояния является накопление полной удельной потенциальной энергии, при этом прочность материала в точке тела будет обеспечена при условии u_расч≤u_R. Здесь u – потенциальная энергия деформации при объемном напряженном состоянии, определяемая по формуле (4.45):

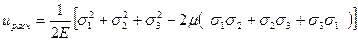(5.10)

u_R – количество потенциальной энергии, накопленной в условиях одноосного напряженного состояния при достижении опасного состояния материала в точке тела, при достижение напряжением значения равного расчетному сопротивлению R:

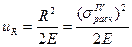(5.11)

Для обеспечения той же безопасности при сложном напряженном состоянии после приравнивания (5.10) и (5.11) получим:

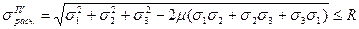(5.12)

В таком виде гипотеза опытным путем не подтвердилась и имеет сейчас только историческое значение, но явилась основой для создания четвертой (энергетической) теории прочности, которая экспериментально подтвердилась достаточно хорошо. Согласно этой теории предполагается, что причиной возникновения опасного состояния является не вся потенциальная энергия, только та её часть, которая накапливается только за счет изменения формы тела, т.е. 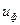≤ 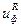. Так как

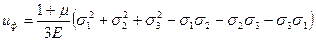; (5.13)

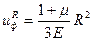; (5.14)

в окончательном виде энергетическая теория прочности выглядит так:

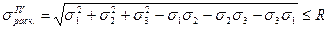(5.15)

В случае плоского напряженного состояния, когда σ₃=0, получим:

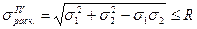. (5.16)

В частном случае плоского напряженного состояния (при поперечном изгибе балок), когда на исходных площадках σ_z=σ, σ_y=0, τ_zy=τ получим:

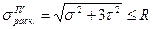(5.17)

Приведенные теории прочности могут быть применены при практических расчетах в зависимости от состояния материала. Для хрупкого состояния материала может быть применена теория наибольших относительных удлинений: при проверке прочности таких материалов как камень, чугун и т.п. Для пластичного состояния материалов целесообразнее применять энергетическую теорию прочности в зависимости от вида напряженного состояния (5.15), (5.16) или (5.17). Все эти соображения применимы только для упругих изотропных материалов.