Закон парности касательных напряжений
Рассмотрим равновесие малого выделенного элемента из твердого деформируемого тела, показанного на рис.4.1. Запишем уравнения равновесия для пространственной системы сил в виде:
ΣМz=0: 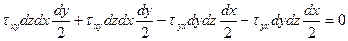 ,
,
ΣМх=0: 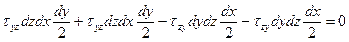 ,
,
ΣМу=0: 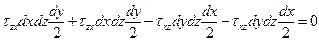
откуда получаем:
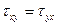
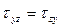 (4.2)
(4.2)
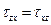
Таким образом, касательные напряжения τ на паре взаимно перпендикулярных площадок равны по величине и направлены к общему ребру или от него. В этом состоит суть закона взаимности или парности касательных напряжений, выражающийся формулами (4.2).
4.3. Напряжения на наклонных площадках при объёмном и при плоском напряженных состояниях
 |
Отсечем от элементарного объёма некоторую его часть произвольной наклонной плоскостью. Положение этой плоскости зададим вектором единичной нормали ν (рис.4.4), с направляющими косинусами:
l=cos(x,ˆν)= 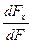 , m=cos(y,ˆν)=
, m=cos(y,ˆν)= 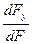 , n=cos(z,ˆν)=
, n=cos(z,ˆν)= 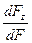
Рассмотрим равновесие полученной элементарной пирамиды. Запишем уравнения равновесия в виде суммы проекций всех сил на координатные оси. Так Σx=0, Σy=0, Σz=0 дают следующую систему уравнений:
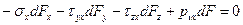
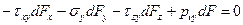
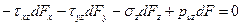
 |  |
С учетом значений направляющих косинусов l, m, n получим значения составляющих полного напряжения рν на наклоной площадке с нормалью ν:
 |
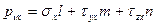
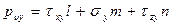 (4.3)
(4.3)
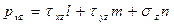
Если наклонная площадка принадлежит поверхности тела, то формулы (4.3) по существу связывают поверхностные нагрузки с компонентами тензора напряжений.
Полное напряжение на наклоной площадке, таким образом, можно определить через его составляющие:
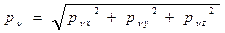 (4.4)
(4.4)
Проектируя составляющие полного напряжения рν (4.3) на нормаль ν, получим с учетом значений направляющих косинусов и закона парности касательных напряжений (4.2) формулу для определения нормальных напряжений на произвольной наклонной площадке при объемном напряженном состоянии:
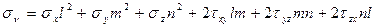 (4.5)
(4.5)
Теперь можно определить и касательные напряжения на наклонной площадке:
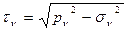
Рассмотрим частный случай плоского напряженного состояния, когда 
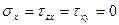 , изображенный на рис.4.5. В этом случае формулы (4.3) примут более простой вид:
, изображенный на рис.4.5. В этом случае формулы (4.3) примут более простой вид:
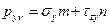 ,
, 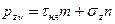 (4.6)
(4.6)
Направляющие косинусы: 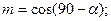
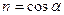
Нормальные напряжения на наклонной площадке с нормалью ν будут равны:
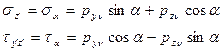 (*)
(*)
C учетом зависимостей (4.6) формулы (*) можно представить в окончательном виде:
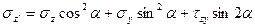 (4.7)
(4.7)
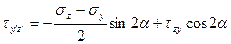 (4.8)
(4.8)
На заштрихованной площадке, для которой β=90+α, значения нормальных и касательных напряжений будут определяться по формулам:
σy' = σzsin2α+σycos2α-τzysin2α (4.9)
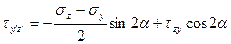 (4.10)
(4.10)
Cкладывая формулы (4.7) и (4.9) получаем:
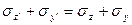 (4.11)
(4.11)
Формула (4.11) выражает мысль о том, что сумма нормальных напряжений на паре взаимно перпендикулярных площадок есть величина постоянная, а формулы (4.8) и (4.10) ещё раз подтверждают закон парности касательных напряжений.
4.4. Главные площадки и главные напряжения при объёмном и плоском напряженном состоянии
При повороте элементарного объёма относительно точки М компоненты тензора напряжений (4.1), как показывают формулы (4.5 – 4.8) , изменяются, т.е., их значения зависят от ориентации элементарного объёма в пространстве. Можно указать такую его ориентацию, при которой на наклонной площадке с внешней нормалью ν касательные напряжения τy'z' окажутся равными нулю.
Площадки, на которых отсутствуют касательные напряжения, называются главными площадками, а нормальные напряжения, действующие на них, называются главными напряжениями.
 Пусть на исходных площадках действуют компоненты тензора напряжений (рис. 4.4). Найдем при этом положение главных площадок и значения главных напряжений на них.
Пусть на исходных площадках действуют компоненты тензора напряжений (рис. 4.4). Найдем при этом положение главных площадок и значения главных напряжений на них.
Предположим, что наклонная площадка с нормалью ν является главной с одним нормальным напряжением σν=σ(i), (i=1,2,3).
Рассматривая в равновесии выделенную пирамиду, т.е., проектируя все силы на оси координат х, у, z получим
-σxdFx + σdFl +τyxdFy+ τzxdFZ = 0
-σydFy + σdFm+τ xydFx +τzydFz = 0
-σzdFz + σdFn+τxzdFx +τyzdFy = 0:
Разделив последние три равенства на площадь наклонной площадки dF, получим три однородных линейных алгебраических уравнения относительно направляющих косинусов l, m, n:
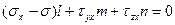 ,
,
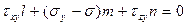 , (4.12)
, (4.12)
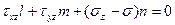 .
.
Система уравнений не должна иметь нулевое решение в силу того, что сумма квадратов направляющих косинусов равна единице, т. е.:
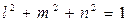 (4.13)
(4.13)
Тогда определитель системы уравнений (4.12)
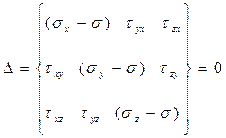 (4.14)
(4.14)
Раскрывая определитель системы уравнений (4.14), получим кубическое уравнение относительно нормального напряжения на главной площадке:
σ3–J1(Тσ)σ2 + J2(Тσ)σ – J3(Тσ) = 0 (4.15)
Коэффициенты при напряжении σ в уравнении (4.15):
J1(Тσ)=σx +σy +σz;
J2(Тσ)=σxσy +σyσz + σzσx–τxy2-τyz2-τxy2 (4.16)
J3(Тσ)=σxσyσz +2τxyτyzτzx–σxτyz2-σyτzx2- σzτxy2
называются первым, вторым и третьим инвариантами напряженного состояния, т.е., величинами, не зависящими от преобразования координат относительно вращения элементарного объёма.
Кубическое уравнение (4.15) имеет три действительных корня, значения, которых расположим в такой последовательности: σ1≥ σ2 ≥ σ2. Напряжения σ1, σ2 , σ3 будут главными, значения их не зависят от операции вращения. Поэтому они будут являться инвариантами а, следовательно, формулы (4.16) можно выразить через главные напряжения:
J1(Тσ)=σ1 +σ2+σ3
J2(Тσ)=σ1σ2+σ2σ3+σ3σ1 (4.17)
J3(Тσ)=σ1σ2σ3
Рассмотрим частный случай, когда σx=τxy=τzx=0 (рис. 4.5). В таком случае инварианты тензора напряжений (4.16) будут равны:
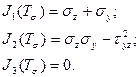 (**)
(**)
Кубическое уравнение (4.15) с учетом (**) преобразуется в квадратное уравнение:
σ2 – J1(Тσ)σ + J2(Тσ)=0 (4.19)
Найдем корни квадратного уравнения (4.19):
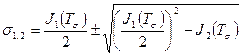 (4.20)
(4.20)
После подстановки значений первого и второго инвариантов (4.18) в формулу (4.20) и выполнения элементарных преобразований получим:
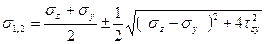 (4.21)
(4.21)
Формула (4.20) применяется при определении главных напряжений при плоском напряженном состоянии. В случае если нормальные напряжения σy=0, значения главных напряжений

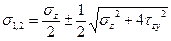 (4.22)
(4.22)
Теперь определим положение главных площадок.
Рассмотрим равновесие выделенного элемента (рис.4.7), с действующими на него главными напряжениями σ1,2 и напряжениями на исходных площадках.
Спроектируем все силы на ось у получим:
σ1,2dFsinα1,2 +τzydFz–σydFy=0
Разделив на dFsinα1,2 последнее равенство, получим:
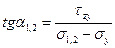
 , (4.23)
, (4.23)
или в частности, когда σy=0:
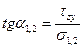 (4.24)
(4.24)
Формулы (4.24) и (4.25) используются для определения положения главных площадок при плоском напряженном состоянии.
Положительный угол α1,2 откладывается от положительного направления оси z против хода часовой стрелки. При этом должно выполняться условие ортогональности главных площадок: сумма модулей углов α1, α2 должно равняться 90об т. е.:
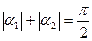
Это указывает на то, что главные площадки, как и исходные площадки взаимно перпендикулярны между собой.
4.5. Экстремальные касательные напряжения при объёмном и плоском напряженном состоянии
В качестве исходных площадок примем главные площадки с главными напряжениями σ1 и σ2 (рис.4.8).Формулы нормальных и касательных напряжений (4.7) и (4.8) принимают вид:
σz'=σ1cos2α+σ2sin2α (4.25)
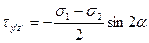 (4.26)
(4.26)
Из формулы (4.26) видно, что при α= ± π/4 касательные напряжения τy'z' принимают экстремальное значение:
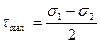 , (4.27)
, (4.27)
или после подстановки главных напряжений (4.21) получим
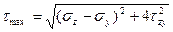 (4.27)*
(4.27)*
Нормальные напряжения:
σ45 = (σ1+σ2)/2 (4.28)
Площадки, где действуют экстремальные касательные напряжения τmax, называются площадками сдвига. На площадках сдвига касательные напряжения равны полу разности главных напряжений, а нормальные напряжения равны полу сумме главных напряжений.
В частном случае, когда на исходных площадках действуют главные напряжения σ1=σ, σ2= -σ экстремальные касательные напряжения:
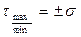 , (4.29)
, (4.29)
а нормальные напряжения σ45 = 0.
Площадки, где действуют только касательные напряжения, назывются площадками чистого сдвига.
 |
В случае объёмного напряженного состояния значения экстремальных касательных напряжений на площадках сдвига нужно определять по формулам:
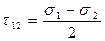 ,
, 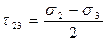 ,
, 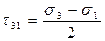 , (4.30)
, (4.30)
а величины нормальных напряжений можно находить так:
σ12 = (σ1+σ2)/2;
σ23 = (σ2+σ3)/2; (4.31)
σ31 = (σ3+σ1)/2.
Таким образом на площадках сдвига действующие касательные напряжения равны полуразности главных напряжений, а нормальные напряжения равны их полусумме.
4.6. Обобщенный закон Гука при объёмном и плоском напряженном состоянии
Из теории простого растяжения известно, что относительная продольная и относительная поперечная деформации для изотропного однородного бруса определяется так:
ε=σ/Е, ε'=-μσ/Е (4.32)
в случае объёмного напряженного состояния действует не одно, а три главных напряжения.
Для определения относительных деформаций по направлению главных напряжений применим принцип суперпозиции. Пусть сначала действует только главное напряжение σ1.
Тогда значения деформаций по направлениям главных напряжений:
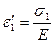
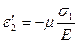
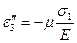 (4.33)
(4.33)
При действии главных напряжений σ2 и σ3 будем иметь аналогичные равенства:
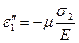
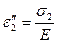
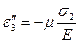 (4.34)
(4.34)
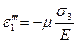
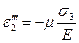
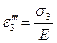 (4.35)
(4.35)
Складывая соответствующие составляющие деформаций (4.33), (4.34) и (4.35) получим:
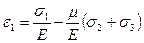
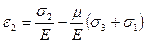 (4.36)
(4.36)
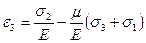
Формулы (4.36) являются обобщенным законом Р. Гука при объёмном напряженном состоянии.
Для случая плоского напряженного состояния, когда одно из главных напряжений, например σ3=0, формулы (4.36) принимают вид:
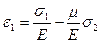 ;
; 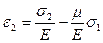 ;
; 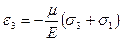 (4.37)
(4.37)
Формулы (4.37) показывают, что при плоском напряженном состоянии деформированное состояние сохраняется объёмным.
4.7. Относительное изменение объёма тела
 |
Рассмотрим деформацию элементарного параллелепипеда с первоначальным объёмом dV0=dx1dx2dx3 при действии на него трех главных растягивающих напряжений σ1≥ σ2≥ σ3 (рис. 4.10а).
После деформации тела (рис.4.10б) его размеры будут такими:
 dV=dx1 dx2 dx3 (1+ε1) (1+ε2) (1+ε3)
dV=dx1 dx2 dx3 (1+ε1) (1+ε2) (1+ε3)
Раскрывая скобки, получим:
dV=(1+ε1+ε2+ε3+ε1ε2+ε2ε3+ε3ε1++ε1ε2ε3)dx1dx2 dx3
Пренебрегая величинами 2-го и 3-го порядка малости, можно записать:
dV≈(1+ε1+ε2+ε3)dx1 dx2 dx3
Относительным изменением объема тела называется отношение разности объёмов после и до деформации к его первоначальному объёму:
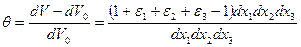
И окончательно получаем, что относительное изменение объёма тела будет равно сумме главных относительных деформаций
Θ=ε1+ε2+ε3 (4.38)
Заменяя в формуле (4.38) относительные деформации в соответствии с формулами обобщенного закона Р. Гука, можно получить:
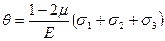 (4.39)
(4.39)
Относительное изменение объёма θ пропорционально первому инварианту тензора напряжений I1(Tσ), а, следовательно, является также инвариантом относительно преобразования вращения элементарного объёма. Кроме того, из формулы (4.39) следует, что коэффициент Пуассона μ не может быть больше 0,5. Подумайте, почему?
Перепишем формулу (4.39) несколько иначе:
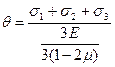
Вводя обозначения
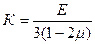 , (4.40)
, (4.40)
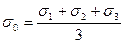 , (4.41)
, (4.41)
запишем
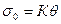 (4.42)
(4.42)
Таким образом, среднее напряжение σ0 пропорционально относительному изменению объёма.
Коэффициентом пропорциональности здесь является модуль объемной деформации К, которыйпо величине несколько ниже модуля нормальной упругости Е.
Следует обратить внимание на то, что при объёмном напряженном состоянии, как и при простом растяжении, существует аналогичная зависимость в форме закона Гука (4.42).
Дата добавления: 2015-12-11; просмотров: 2286;
