Потенциальная энергия упругой деформации при сложном напряженном состоянии

Из теории простого растяжения и сжатия известно, что удельная потенциальная энергия упругой деформации определяется по формуле:

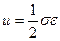(4.43)

Обобщая формулу (4.43) на случай объёмного напряженного состояния, когда действует не одно, а три главных напряжения, удельную потенциальную энергию можно определить так:

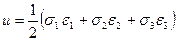(4.44)

Используя формулы обобщенного закона Р.Гука (4.36), формулу (4.44) можно представить в таком виде

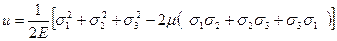(4.45)

В случае плоского напряженного состояния, при σ₃=0 получим

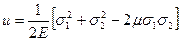(4.46)

Разложим объёмное напряженное состояние на два составляющих: в одном из них будут действовать только средние напряжения σ₀ (рис. 4.11в), а в другом разности напряжений σ'_{i =}σ_i-σ₀(рис.4.11б), (i=1,2,3). Подставим в формулу (4.39) вместо главных напряжений значения σ_i-σ₀получим:

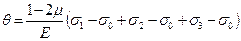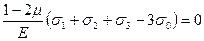= (4.47)

Следовательно, вторая составляющая напряженного состояния не связана с изменением объёма тела, а лишь только с изменением его формы. Первая же составляющая напряженного состояния связана только с изменением объёма тела, которое составит:

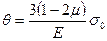(4.48)

Обозначая в формуле (4.48)

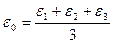, (4.49)

с учетом (4.40) запишем:

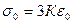(4.50)

Следовательно, среднее напряжение при объёмном напряженном состоянии пропорционально утроенному значению средней деформации. Это еще одна форма записи закона Р.Гука.

A теперь представим потенциальную энергию как сумму энергии изменения объёма u₀ и энергии изменения формы тела:

u = u₀ +u_ф (4.51)

Найдем эти составляющие потенциальной энергии, воспользовавшись формулой (4.45). Подставим туда значение σ₀ (4.41) получим:

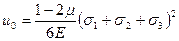(4.52)

Энергия изменения формы тела будет вычисляться разностью u_ф = u - u_0, т.е.:

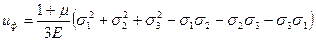(4.53)

в частном случае плоского напряженного состояния, когда σ₃ = 0

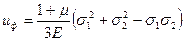(4.54)

В случае, когда на исходных площадках при плоском напряженном состоянии σ_x=τ_xy=τ_xz=σ_y=0, σ_z=σ, τ_yz=τ, с учетом формулы (4.22) потенциальная энергия формоизменения объема тела принимает следующий вид:

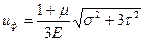(4.55)

Полученные формулы по исследованию напряженного состояния имеют фундаментальное значение в науке сопротивления материалов по созданию теорий прочности при сложном напряженном состоянии для различных материалов.