Обозначение напряжений. Правило знаков. Виды напряженного состояния
 Рассмотрим тело произвольной формы, занимающее объем V (рис. 4.1), в декартовой системе координат x,y,z , определенным образом закрепленное, загруженное некоторой произвольной нагрузкой, находящееся в равновесии. Выделим из этого тела элементарный объём размером dV=dx×dy×dz . По граням этого объёма будут действовать, как известно из вводной части, нормальные σ и касательные τ напряжения рис 4.2.
Рассмотрим тело произвольной формы, занимающее объем V (рис. 4.1), в декартовой системе координат x,y,z , определенным образом закрепленное, загруженное некоторой произвольной нагрузкой, находящееся в равновесии. Выделим из этого тела элементарный объём размером dV=dx×dy×dz . По граням этого объёма будут действовать, как известно из вводной части, нормальные σ и касательные τ напряжения рис 4.2.
Примем следующие обозначения для напряжений:
 нормальное напряжение обозначим буквой σ с одним индексом, означающим название оси, параллельно которой оно действует. Так нормальное напряжение σх направлено параллельно оси х. Касательные напряжения обозначим буквой τ с двумя индексами – первый будет означать ось, которая является нормалью к рассматриваемой площадке элементарного объёма, а второй индекс будет означать ось, параллельно которой это напряжение действует. Так касательное напряжение τyx действует на грани элементарного объёма с нормалью у параллельно оси х.
нормальное напряжение обозначим буквой σ с одним индексом, означающим название оси, параллельно которой оно действует. Так нормальное напряжение σх направлено параллельно оси х. Касательные напряжения обозначим буквой τ с двумя индексами – первый будет означать ось, которая является нормалью к рассматриваемой площадке элементарного объёма, а второй индекс будет означать ось, параллельно которой это напряжение действует. Так касательное напряжение τyx действует на грани элементарного объёма с нормалью у параллельно оси х.
Правило знаков для напряжений:
если внешняя нормаль к рассматриваемой грани (площадке) совпадает с положительным (отрицательным) направлением координатной оси, то положительное напряжение также должно совпадать с положительным (отрицательным) направлением той оси, параллельно которой это напряжение действует. На рис 4.2 все напряжения показаны с положительным знаком.
Меняя ориентацию выделенного объёма относительно осей x, y, z, будут изменяться значения нормальных σ и касательных напряжений τ.
Вся совокупность нормальных и касательных напряжений, действующих по всевозможным площадкам в окрестности данной точки, образуют напряженное состояние в этой точке. Можно указать такое положение элементарного объёма dV относительно осей x, y, z, при котором на его гранях будут отсутствовать касательные напряжения τ. Площадки, где отсутствуют касательные напряжения, называются главными площадками, а нормальные напряжения σ, действующие на главных площадках, называются главными напряжениями.
Если вся совокупность напряжений приводится к одному главному напряжению σ1 – напряженное состояние называется одноосным (линейным – простое растяжение-сжатие: рис 4.3а), к двум главным напряжениям σ1 и σ2 – напряженное состояние считается двуосным (плоским: рис 4.3б), к трем главным напряжениям σ1, σ2, σ3 – напряженное состояние относится к трехосному (пространственному или объёмному) (рис. 4.3в).
 |
Представим совокупность напряжений (рис. 4.2), действующих на исходных площадках малого объёма в виде такой таблицы:
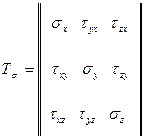 (4.1)
(4.1)
Данная таблица представляет собой тензор напряжений, характеризующий напряженное состояние в точке деформируемого твёрдого тела.
Таким образом, подобно скалярной величине, характеризующейся одним числом и векторной величине, характеризующейся тремя числами (как правило, проекциями на координатные оси), тензорная величина описывается девятью компонентами, содержащимися в таблице (4.1).
Дата добавления: 2015-12-11; просмотров: 1861;
