Потенциальная энергия при растяжении и сжатии

Сила P, приложенная к стержню постоянного сечения, вызывает перемещение его нижней точки на величину Δl (рис. 3.32 а). Эта сила P на перемещении Δl совершает работу. В элементе при этом накапливается потенциальная энергия. После снятия внешней нагрузки потенциальная энергия восстанавливает стержень в первоначальных размерах.

Потенциальная энергия деформации – энергия, обусловленная работой внешних сил, приложенных к элементу, на вызванных ими перемещениях.

На рис 3.32 б показана диаграмма растяжения стали. Приложенная сила P₁ вызывает удлинение стержня на величину Δl₁. После приращения силы на величину ΔP₁ деформация его увеличивается на dΔl₁. Элементарную работу силы P₁ в пределах упругих деформаций можно найти как произведение

dA = P₁dΔl₁

Согласно рис 3.32 б это произведение есть элементарная площадка dω.

dA = dω

Или

A = 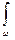dω = ω

Следовательно, работа внешней силы или потенциальная энергия, накопленная стержнем в пределах упругих деформаций, равна площади треугольника:

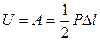(3.27)

Учитывая, что продольное усилие N = P, а абсолютная деформация

,

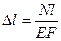получим:

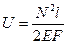(3.28)

В случае ступенчатого стержня, имеющего n участков, величина потенциальной энергии может быть найдена как

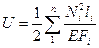(3.29)

В теоретической части курса «Сопротивление материалов» используется понятие так называемой удельной потенциальной энергии деформации.

Удельная потенциальная энергия представляет собой величину потенциальной энергии, накопленной стержнем в процессе деформации, отнесенной к единице объема материала.

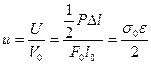
здесь

,

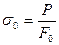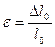
Относительную деформацию через напряжения по закону Гука можно найти как:

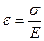
Следовательно, 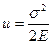(3.31)