Статически неопределимые задачи при растяжении и сжатии
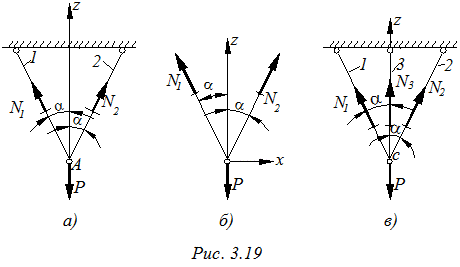
Закрепим груз P с помощью двух стержней 1 и 2 (рис. 3.19а). Неизвестные усилия в стержнях можно определить, рассмотрев в равновесии узел «А» (рис. 3.19в). Записав два уравнения, статики найдем усилия N1 и N2.
ΣFz = 0 N1 cos α + N2 cos α – P = 0
ΣFz = 0 N1 sin α - N2 sin α = 0 отсюда N1 = N2
2N1 cos α = P, или 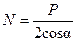 .
.
Теперь добавим в узел «А» вертикальный стержень 3 (рис.3.19с). Три неизвестные усилия N1, N2 и N3 нельзя найти с помощью двух уравнений статики (система сил сходящая). В этом случае говорят, что задача статически не определима.
Статически неопределимой называется такая система, усилия в которой не возможно определить с помощью уравнений статики.
Степень статической неопределимости системы - разница между количеством неизвестных и количеством возможных уравнений статики называется
Уравнения перемещений (деформаций) - дополнительные уравнения, которые составляют для решения статически неопределимых систем.
Количество таких уравнений соответствует степени статической неопределимости системы.
 |
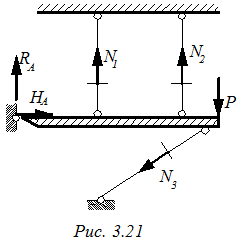
Степень статической неопределимости η для простых случаев загружения можно определить как (рис. 3.20 и 3.21):
А) Сходящая система сил η = S – 2U
S – число стержней;
U – количество внутренних узлов.
Для системы, изображенной на (рис 3.20) η = 5 - 2·2 = 1, следовательно, система один раз статически неопределима.
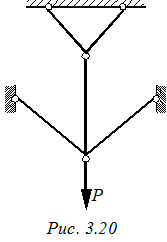
В) Плоская система сил η = n - 3
n – количество неизвестных;
3 – количество уравнений статики для плоской системы сил.
Для системы, изображенной на (рис 3.21) η = 5 – 3 = 2, следовательно, система два раза статически неопределима.
| A) Сходящая система сил | В) Плоская система сил |
|
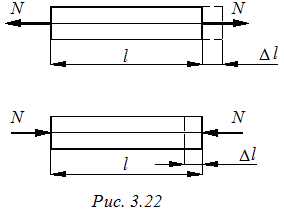 При решении таких задач необходимо следить за тем, чтобы соблюдалось условие совместности перемещений (рис.3.22).
При решении таких задач необходимо следить за тем, чтобы соблюдалось условие совместности перемещений (рис.3.22).
при растяжении стержень должен удлиняться,
при сжатии стержень должен укорачиваться.
Если на схеме перемещений это условие не выполняется, перед соответствующей деформацией ставится знак минус.
При решении статически неопределимых задач рассматривают следующие три стадии:
1. Статическая сторона задачи,
2. Геометрическая сторона задачи,
3. Физическая сторона задачи.
Рассмотрим решение статически неопределимых задач на следующих примерах.
Пример № 3.2
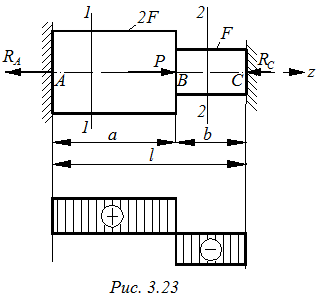 Определить напряжения на участках ступенчатого бруса, закрепленного двумя концами, от действия силы Р (рис. 3.23).
Определить напряжения на участках ступенчатого бруса, закрепленного двумя концами, от действия силы Р (рис. 3.23).
Данная задача один раз статически неопределима, так как для нахождения двух неизвестных реакций Ra и Rc имеем только одно уравнение статики (система сил линейная).
1. Статическая сторона задачи
ΣFz = 0 Ra + Rc = P (a)
2. Геометрическая сторона задачи
До приложения нагрузки длина стержня равнялась l. Так как в точках А и В стержень защемлен, то и после приложения нагрузки длина останется прежней.
Следовательно, Δl = 0.
Учитывая, что общая деформация состоит из деформаций двух участков, запишем:
Δlобщ = Δla + Δlb = 0.
3. Физическая сторона задачи
Заменяем деформации через усилия по закону Гука:
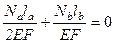 , отсюда Nala + 2Nblb = 0 (b)
, отсюда Nala + 2Nblb = 0 (b)
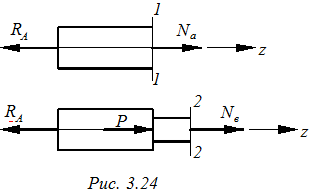 Пользуясь методом сечений, выразим усилия Na и Nb через реакцию
Пользуясь методом сечений, выразим усилия Na и Nb через реакцию  Ra, чтобы не решать систему двух уравнений (рис.3.24).
Ra, чтобы не решать систему двух уравнений (рис.3.24).
Подставим найденные значения усилий в уравнение (b).
Rala + 2·(Ra - P)lb =0
Отсюда
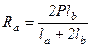
Теперь можно найти неизвестные усилия, подставив найденное значение реакции в уравнения (с) и (d):
Na = Ra = 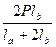 Nb = Ra – P = –
Nb = Ra – P = – 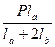
Следовательно, на участке длиной la стержень растянут, а на участке длиной lb - сжат. Теперь окончательно становится ясным физический смысл уравнения деформаций: удлинение участка стержня длиной lalb равно укорочению участка длиной lb.
Пример № 3.3
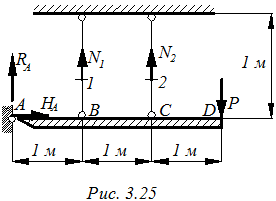 Абсолютно жесткий брус АD закреплен при помощи шарнира А и двух стальных стержней 1 и 2. Площади стержней одинаковы. Определить усилия в этих стержнях от заданной нагрузки P=20кН (рис. 3.25).
Абсолютно жесткий брус АD закреплен при помощи шарнира А и двух стальных стержней 1 и 2. Площади стержней одинаковы. Определить усилия в этих стержнях от заданной нагрузки P=20кН (рис. 3.25).
В данной задаче четыре неизвестных (Ra, Ha, N1, N2), для нахождения которых имеем три уравнения статики.
Следовательно, 4 – 3 =1
Система один раз статически неопределима.
1. Статическая сторона задачи
Из трех уравнений статики берем одно, в которое не входят реакции Ra и Ha.
ΣMa = 0 N11 + N22 – P3= 0 или N11 + N22 = P3 (a)
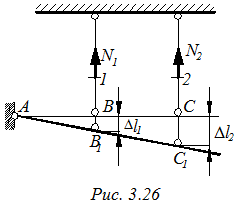 2. Геометрическая сторона задачи (рис. 3.26)
2. Геометрическая сторона задачи (рис. 3.26)
Для нахождения зависимости между деформациями стержней строим план перемещений (рис. 3.26). Ввиду малости деформаций перемещения по дуге BB1 заменяем перемещениями по хорде BB1. Из подобия треугольников ABB1 и ACC1, найдем:
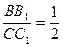 или,
или, 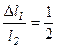 следовательно, Δl1 = Δl2
следовательно, Δl1 = Δl2
2. Физическая сторона задачи:
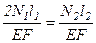 или 2N1 – N2 = 0 (b)
или 2N1 – N2 = 0 (b)
Решаем совместно уравнения (а) и (в)
2N1 – N2 = 0
N1 + N22= 0
N1 = 12 кН, N2 = 24 кН
Для проверки решения найденные значения усилий подставим в уравнение (в)
12 + 2·24 = 20·3 60 = 60
Пример № 3.4
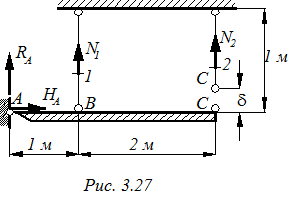 Абсолютно жесткая балка АС закреплена при помощи шарнира А и двух стальных стержней 1 и 2. Стержень 2 был изготовлен короче требуемой длины на величину
Абсолютно жесткая балка АС закреплена при помощи шарнира А и двух стальных стержней 1 и 2. Стержень 2 был изготовлен короче требуемой длины на величину 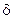 . При сборке системы он был поставлен на место с предварительным растяжением. В результате этого появилось усилие и в стержне 1. Площади стержней одинаковы. Требуется определить усилия в стержнях 1 и 2 (рис. 3.27).
. При сборке системы он был поставлен на место с предварительным растяжением. В результате этого появилось усилие и в стержне 1. Площади стержней одинаковы. Требуется определить усилия в стержнях 1 и 2 (рис. 3.27).
В данной задаче четыре неизвестных (Ra, Ha, N1, N2), для нахождения которых имеем три уравнения статики.
4 – 3 = 1 система один раз статически неопределима.
1. Статическая сторона задачи
ΣMa = 0 N11 + N23= 0 или N11 + 3N2 = 0 (a)
2. 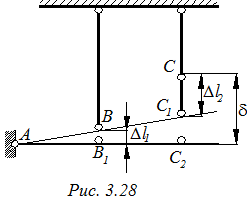 Геометрическая сторона задачи (рис. 3.28)
Геометрическая сторона задачи (рис. 3.28)
Из подобия треугольников ABB1 и AC2C1, найдем:
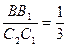 или,
или, 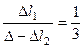 следовательно,
следовательно,
-3Δl1 + Δl2 = Δ
Перед Δl1 поставлен минус, так как на плане сил усилие показано растягивающим, а на плане перемещений стержень укорачивается.
3. Физическая сторона задачи:
- 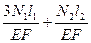 = Δ или 3N1 + N2 =
= Δ или 3N1 + N2 = 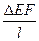 (b)
(b)
Решив совместно уравнения (а) и (b) найдем усилия N1 и N2:
N1 = 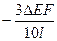 N2 =
N2 = 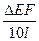
Следовательно, в результате сборки стержень 1 будет сжат, а стержень 2 – растянут.
Пример №3.5
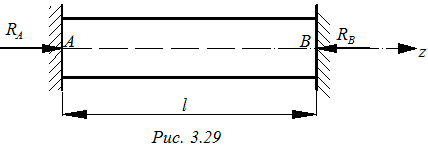 Призматический брус длиной l жестко закреплен в точках А и В. Стержень по всей длине нагревается на
Призматический брус длиной l жестко закреплен в точках А и В. Стержень по всей длине нагревается на 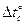 . Определить температурные напряжения в стержне (рис. 3.29).
. Определить температурные напряжения в стержне (рис. 3.29).
При нагревании стержень стремится удлинится на величину Δlt. Закрепления в точках А и В препятствуют температурному удлинению. Следовательно, в сечениях стержня возникают температурные напряжения.
В данной задаче две неизвестных опорных реакции Ra и Rb не могут быть найдены с помощью одного уравнения статики. Система сил линейная
Следовательно, 2 - 1 = 1 - задача один раз статически неопределима.
1. Статическая сторона задачи
ΣFz = 0 Ra – Rb = 0 (a)
2. Геометрическая сторона задачи
Δlобщ = 0 или Δlt + ΔlN = 0
3. Физическая сторона задачи
αΔ 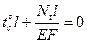
α - коэффициент линейного расширения материала. Определяется по таблице, размещенной в блоке справочных данных.
Сокращая выражение (b) на величину l и, учитывая, что 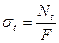 , получим:
, получим:
σТ = - EαΔ 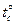 .
.
Знак минус говорит о том, что при нагревании в защемленном стержне возникают сжимающие напряжения.
Дата добавления: 2015-12-11; просмотров: 2961;
