Теория прочности Отто-Мора

Теория прочности О. Мора основана на использовании кругов напряжений. При трехосном напряженном состоянии строят три круга напряжений (рис. 5.1). Как показывают экспериментальные исследования, промежуточные главные напряжения σ₂ мало оказывают влияние на прочностные свойства материалов. Ошибка от их не учета составляет около 10-15%. Поэтому можно считать, что прочностные свойства материала зависят только от наибольшего σ₁ и наименьшего σ₃ главных напряжений. Поэтому из трех кругов во внимание принимают во внимание лишь один – наибольший, который называется главным кругом.

В случае, когда главные напряжения σ₁ и σ₃ соответствуют предельному напряженному состоянию материала, соответствующий им главный круг называют также предельным. На рис. 5.2 представлены три предельных круга для материала, который был подвержен испытанию на растяжение, сжатие (красный цвет) и кручение (синий цвет). Предельное напряжение при сжатии обозначено через σ_ос, которое больше чем при растяжении σ_ор.

Огибающая, проведенная к этим кругам напряжений, называется предельной огибающей. Эта кривая пересекает ось σ в точке Е. Точка Е соответствует всестороннему равномерному растяжению. Здесь главные напряжения σ₁=σ₂=σ₃.

Таким образом, если другое напряженное состояние, главный круг которого касается огибающей, будет также предельным.

На рис. 5.2 черным цветом показаны два предельных круга с различными сочетаниями главных напряжений. Словом, огибающая кругов определяет зависимость этих напряжений от вида напряженного состояния. Получение действительной огибающей предельных кругов, построенных для всевозможных сочетаний главных напряжений практически невозможно, так как потребовалось бы проведение огромного количества опытов. Поэтому на практике действительную огибающую заменяют прямыми касательными лишь к двум кругам, которые строят по данным опыта на растяжение и сжатие (рис. 5.3). Эти прямые являются границами прочностных состояний. Кроме того, с их помощью между напряжениями σ₁ и σ₃ устанавливается линейная зависимость для любого напряженного состояния, главный круг которых касается этих прямых в виде:

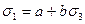(5.18)

Из подобия прямоугольных треугольников А₁С₁С₂ и А₂С₂С₃ следует:

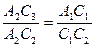(а)

где

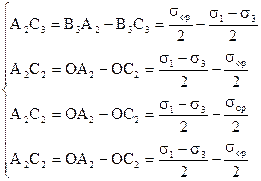(б)

Подставим значения (б) в формулу (а) получим:

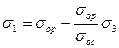(5.19)

В силу полученных результатов расчетная формула в соответствии с теорией прочности Мора запишется так:

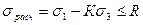(5.20)

Коэффициент К позволяет учитывать различные сопротивления материала растяжению и сжатию. Если эти сопротивления равны между собой, то К=1, а касательные к главным кругам становятся параллельными к оси σ (рис. 5.4).

Условие прочности Мора (5.24) будет совпадать с уловием третьей теории прочности. Следовательно оно применимо как для хрупких так и для пластичных материалов. При этом следует для хрупких материалов принимать вместо σ_ос и σ_ор значения пределов прочности при сжатии и растяжении, а для пластичных материалов – пределы текучести.

Теория Мора дает наиболее достоверные результаты для напряженных состояний, круги которых занимают положение в промежутке между главными кругами при растяжении и сжатии.