Объединенная теория прочности
Эта теория прочности два вида разрушения материала: хрупкое, происходящее путем отрыва, и вязкое возникающее от среза (сдвига). Идея этой была предложена в 1936 году проф. Н.Н. Давиденковым и в дальнейшем развита Я.Б. Фридманом.
Объединенная теория прочности объединяет между собой вторую и третью теории прочности и позволяет приближенно установить характер и причину разрушения материала.
Напряжение, при котором происходит разрушение за счет отрыва, обозначим через σотр, а напряжение, соответствующее разрушению при сдвиге, - обозначим τраз.
Примером хрупкого разрушения может служить разрушение чугунного стержня при кручения, характерным отрывом, происходящим по главным площадкам от растягивающих напряжений. К вязкому разрушению можно отнести разрушение вала, изготовленного из пластичной стали.
Предложенные ранее первая и вторая теории прочности могут быть отнесены к группе теорий, объясняющих разрушение материала как явление отрыва, а третья и энергетическая теории прочности можно отнести к другой группе теорий объясняющих, что разрушение происходит за счет деформации среза.
В свое время считалось, что материал может разрушаться либо путем отрыва, либо за счет среза.
Объединенная теория прочности исходит из эксперементально обоснованной гипотезы о том, что разрушение материала может происходить как за счет отрыва так и за счет сдвига в зависимости от условий работы и вида напряженного состояния.
Для этого строится так называемая диаграмма механического состояния, которая позволяет исследовать одновременно прочность исследуемого на отрыв и на сдвиг и установить вид возможного разрушения (рис.5.5). Эта диаграмма строится в осях τmax и σmax в форме прямоугольника, ограничивающего область прочных состояний для данного материала (рис. 5.5а)
 |
Построение этого прямоугольника основано на предположении о том, что определяемые из опыта значения напряжений σотр и τраз для каждого материала постоянны и не зависят от вида напряженного состояния.. Н этом же графике дается прямая, соответствующая началу текучести τТ. Эта прямая делит всю область прочного состояния на две зоны, одна из которых расположенных ниже прямой, относится к упругим деформациям, другая – к пластическим. На (рис. 5.5б) показана кривая, которая строится по данным опыта в системе координат τmax и γmax. На этой кривой фиксируются точки, соответствующие пределу текучести, т.е. началу появления пластических деформаций и разрушению материала, которые используются при построении графика, изображенного на (рис 5.5, а).
При исследовании напряженного состояния по оси σmax откладывается величина наибольшего растягивающего напряжения, которое определяется в соответствии со второй теорией прочности по формуле:
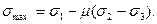 (а)
(а)
По оси τmax откладываются расчетная величина наибольшего касательного напряжения в соответствии с теорией наибольших касательных напряжений:
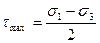 (б)
(б)
Следовательно, каждое напряженное состояние на графике отображается точкой, характеризующейся отношением:
 , (в)
, (в)
например, точками 1, 2 или 3 (рис. 5.5а). Указанное отношение (в) является основной характеристикой напряженного состояния. Измененяя интенсивность последнего при m= const, получим на графике луч, выходящий из начала координат, который наклонен к оси σmax под углом δ, тангенс которого равен m. При построении такого луча делается предположение о том, что он будет оставаться прямым и при переходе материала в пластическую стадию вплоть до его разрушения.
Если на графике провести лучи ОА и ОВ под углами α β к оси σmax, которые соответствуют отношениям 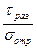 и
и  , то для различных напряженных состояний, характеризующихся отношением m будем иметь:
, то для различных напряженных состояний, характеризующихся отношением m будем иметь:
а) при δ >α – разрушение за счет среза ( луч Ос);
б) при β < δ <α - разрушение засчет отрыва, которое произойдет после развития пластических деформаций (луч Оd);
в) при δ < α – разрушение произойдет за счет отрыва без развития пластических деформаций (луч Ое).
Так для различнызх материалов и в разных условиях их работы предельное значения напряжений неодинаковы, то линии отрыва и среза будут располагаться на разных расстояниях от координатных осей. Следовательно, при одном и том же напряженном состоянии могут иметь месть разные виды разрушения, а поэтому должны назначаться нединаковые коэффициенты запаса.
Таким образом, отношение m позволяет в каждом отдельном случае приближенно устанавливать вероятный вид разрушения, а также степень его близости к другому виду и на основании этого принимать тот или иной коэффициент запаса. Так если напряженное состояние характеризуется лучом Ос, то очевидно, коэффициент запаса следует назначать по отношению к пределу текучести τТ, а при луче Ое – по отношению к σотр.
Данная теория может применяться для приближенного решения вопросов о возможном виде разрушения материалов и их поведении при различных заданных условиях.
Однако, несмотря на приближенность этой теории прочности, она имеет важный практический интерес, как наиболее простая и удачная, позволяющая схематизировать сложнейшие явления, которые сопутствуют разрушению материалов.
Дата добавления: 2015-12-11; просмотров: 2166;
