Напряжения и деформации при чистом сдвиге. Закон Р. Гука
Деформация чистого сдвига без других видов сопротивления встречается крайне редко. Обычно чистый сдвиг сочетается с каким-либо другим видом деформации: растяжением, сжатием, изгибом. Все это усложняет изучение этого простого вида деформации.
Рассмотрим короткую консоль длиной а, загруженную поперечной нагрузкой Q, равномерно распределенной по площади поперечного сечения F этой консоли. В такой консоли влиянием явления изгиба с достаточной степенью точности можно пренебречь.
Задачу будем рассматривать в рамках гипотезы плоских сечений и гипотезы о малости перемещений. Кроме того, будем считать, что продольные волокна короткого бруса не деформируются и не взаимодействуют между собой в поперечном направлении. Поэтому в нем не возникают нормальные напряжения σ, а лишь только касательные напряжения τ. Таким образом, данный брус находится в условиях чистого сдвига. При равномерном распределении силы Q и малости длины а консоли в любом её сечении, касательные напряжения τ, можно находить по формуле:
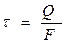 (6.1)
(6.1)
 В результате действия приложенной нагрузки форма консоли измениться. Её вид после деформации показан на рис. 6.1 штриховой линией. Величина линейного перемещения Δh=кк׳ угловой точки к консоли называется абсолютным сдвигом. Первоначально прямой угол консоли изменится на величину γ. Отношение
В результате действия приложенной нагрузки форма консоли измениться. Её вид после деформации показан на рис. 6.1 штриховой линией. Величина линейного перемещения Δh=кк׳ угловой точки к консоли называется абсолютным сдвигом. Первоначально прямой угол консоли изменится на величину γ. Отношение 
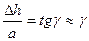 (6.2)
(6.2)
называется относительным сдвигом. Между касательными напряжениями τ и относительным сдвигом до определенного значения нагрузки Q наблюдается линейная, т. е. пропорциональная зависимость:
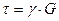 , (6.3)
, (6.3)
где G – модуль упругости II рода, или модуль сдвига. Таким образом, при рассмотрении деформации чистого сдвига наряду с модулем упругости Е и коэффициентом Пуассона μ появилась еще одна постоянная упругости G. Используя формулу (6.2) и (6.1) из формулы (6.3) получим:
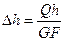 . (6.4)
. (6.4)
Формула (6.4) является второй формой закона Гука, позволяющей определять через заданную нагрузку значение абсолютного сдвига Δh. Произведение GF называется жесткостью бруса при сдвиге, которая характеризует податливость бруса при сдвиге. Чем больше жесткость GF, тем менее брус деформативен и, наоборот, чем меньше жесткость GF, тем брус более деформативен, т. е. материал его слабее сопротивляется изменению его формы.
Деформация чистого сдвига в отдельности, как уже сказано выше, встречается крайне редко. Она, как правило, сочетается с другими видами деформаций, например, со смятием в заклепочных и болтовых соединениях, или является составляющей напряженного состояния балок при поперечном изгибе. Однако в достаточной степени точности можно считать, что сварные фланговые швы или тонкостенная труба при действии на нее скручивающих моментов Мкр находятся в условиях чистого сдвига. Пользуясь этим положением, в лабораторных условиях из опыта на кручение определяют модуль сдвига G.
6.2. Зависимость между модулем сдвига G, модулем продольной упругости E и коэффициентом Пуассона μ
 |
Установим зависимость между модулем сдвига G и модулем нормальной упругости Е. Материал бруса характеризуется коэффициентом Пуассона μ Рассмотрим малый элемент размером аHа с диагональю
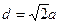 , находящийся в условиях чистого сдвига при действии касательных напряжений τ (рис. 6.2а).Найдем относительное удлинение диагонали этого элемента, как отношение абсолютного удлинения к׳к׳׳ =Δd к первоначальной длине d:
, находящийся в условиях чистого сдвига при действии касательных напряжений τ (рис. 6.2а).Найдем относительное удлинение диагонали этого элемента, как отношение абсолютного удлинения к׳к׳׳ =Δd к первоначальной длине d:
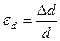 (6.5)
(6.5)
Из рисунка 6.2а видно отрезок кк׳=аγ. Тогда абсолютное удлинение диагонали Δd=кк׳·соs450=аγсоs450= 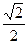 аγ. Подставляя в формулу (6.5) значения Δd и d, получаем:
аγ. Подставляя в формулу (6.5) значения Δd и d, получаем:
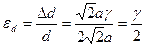 ,
,
а с учетом закона Гука при чистом сдвиге (6.3):
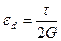 (6.6)
(6.6)
Выразим величину относительного удлинения диагонали εd (рис. 6.2а) через главные напряжения, характеризующие деформацию чистого сдвига: σ1= τ; σ2= -τ (п.5.5 рис. 4.9). Применяя обобщенный закон Гука при плоском напряженном состоянии (4.37), записываем:
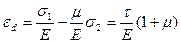 (6.7)
(6.7)
Сравнивая выражения для εd (6.6) и (6.7) имеем:
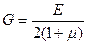 . (6.8)
. (6.8)
Формула (6.8) связывает модуль сдвига G с модулем нормальной упругости Е. Таким образом между тремя упругими постоянными существует одна зависимость. Следовательно, независимых упругих постоянных существует только две. А это дает возможность, определив две из них третью найти по формуле (6.8).
Дата добавления: 2015-12-11; просмотров: 3570;
