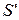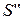Статистичні критерії
Для того, щоб вияснити, чи є співпадання або відмінності випадковими, використовують статистичні методи, які дозволяють на основі даних, отриманих експериментатором, прийняти обгрунтоване рішення про співпадання чи відмінність характеристик. Насамперед, формулюються статистичні гіпотези. Статистичною (її називають ще «нульовою»)  гіпотезою називають передбачення стосовно належ-ності експериментальної вибірки до генеральної сукупності з певними статистичними характеристиками. Зокрема, як нульову гіпотезу
гіпотезою називають передбачення стосовно належ-ності експериментальної вибірки до генеральної сукупності з певними статистичними характеристиками. Зокрема, як нульову гіпотезу  розглядають передбачення, яке стверджує, що вибірки , які вивчаю-ться, взяті з генеральних сукупностей із однаковим законом розподілу, а різниця в результатах вибірок пояснюється виключно випадковими ознаками. Прикладом нульової гіпотези такого типу є ствердження про те, що різниця у результатах виконання двома групами студентів одного й того самого тесту викликана випадковими причинами, а насправді рівень виконання тестової контрольної роботи в обох групах однаковий.
розглядають передбачення, яке стверджує, що вибірки , які вивчаю-ться, взяті з генеральних сукупностей із однаковим законом розподілу, а різниця в результатах вибірок пояснюється виключно випадковими ознаками. Прикладом нульової гіпотези такого типу є ствердження про те, що різниця у результатах виконання двома групами студентів одного й того самого тесту викликана випадковими причинами, а насправді рівень виконання тестової контрольної роботи в обох групах однаковий.
Перевірка нульової гіпотези  переважно виконується шляхом порівняння її з іншою, альтернативною гіпотезою
переважно виконується шляхом порівняння її з іншою, альтернативною гіпотезою 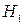 . Зокрема, для наведеного прикладу гіпотези
. Зокрема, для наведеного прикладу гіпотези  альтернативною гіпотезою
альтернативною гіпотезою 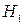 є твердження, що рівні виконання тестової контрольної роботи в обох групах різні, і ця відмінність визначається впливом невипадкових факторів, наприклад, експериментальних методів навчання. Альтер-нативну гіпотезу (чи гіпотези, якщо їх декілька) приймають тоді і лише тоді, коли відкидається нульова гіпотеза.
є твердження, що рівні виконання тестової контрольної роботи в обох групах різні, і ця відмінність визначається впливом невипадкових факторів, наприклад, експериментальних методів навчання. Альтер-нативну гіпотезу (чи гіпотези, якщо їх декілька) приймають тоді і лише тоді, коли відкидається нульова гіпотеза.
Для прийняття рішення про те, яку з гіпотез (нульову чи альтер-нативну) слід прийняти, використовують статистичні критерії – вирішальне правило, на основі якого нульова гіпотеза відхиляється чи приймається. Тобто, на основі інформації про результати спостережень (характеристики членів експериментальної і контрольної груп) вирахо-вується число, яке називають емпіричним значенням критерію. Це число порівнюється з відомим (наприклад, заданим таблично) ета-лонним числом – критичним значенням критерію. Критичні значення наводяться, переважно, на декількох рівнях значущості. Рівнем значу-щості називають ймовірність похибки, яка полягає у відхиленні (не прийнятті) нульової гіпотези, або ймовірність того, що відмінності визначено суттєвими, а в дійсності вони випадкові.
Переважно, рівень значущості статистичного висновку позначають 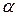 . У педагогічних дослідженнях використовують три рівні значу-щості статистичного висновку:
. У педагогічних дослідженнях використовують три рівні значу-щості статистичного висновку:
- перший рівень – 5% ( 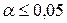 ), де допускається ризик помилки у висновку в п’яти випадках зі 100 теоретично можливих таких самих експериментів при суворо випадковому відборі досліджуваних для кожного експерименту;
), де допускається ризик помилки у висновку в п’яти випадках зі 100 теоретично можливих таких самих експериментів при суворо випадковому відборі досліджуваних для кожного експерименту;
- другий рівень – 1%, тобто допускається ризик помилитися тільки в одному випадку зі 100 ( 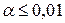 при тих самих вимогах);
при тих самих вимогах);
- третій рівень – 0,1%, тобто допускається ризик помилитися тільки в одному випадку з тисячі ( 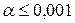 ). Цей рівень значущості обумовлює дуже високі вимоги до обгрунтування результатів експе-рименту, а тому рідко досягається.
). Цей рівень значущості обумовлює дуже високі вимоги до обгрунтування результатів експе-рименту, а тому рідко досягається.
Необхідно вказати, що в педагогічних дослідженнях традиційно обмежуються значенням 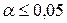 , простіше кажучи, допускається не більше, ніж 5% можливість помилки.
, простіше кажучи, допускається не більше, ніж 5% можливість помилки.
Таким чином, загальний алгоритм використання статистичних критеріїв обумовлюється такою послідовністю дій: до початку і на завершення експерименту на основі отриманих результатів спосте-режень (характеристик членів експериментальної й контрольної груп) вираховується емпіричне значення критерію (методика вибору необхідного критерію та його розрахунок буде наведено у подальших матеріалах). Отримане число порівнюється з відомим (табличним) числом – критичним значенням критерію (Колмогорова-Смірнова, 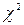 (Хі-квадрат), Макномарі, Крамера-Уелча, Вілконсона-Манна-Уітні, Фішера, Стьюдента тощо). Якщо емпіричне значення критерію вияв-ляється меншим або дорівнює критичному, то можна стверджувати, що характеристики експериментальної та контрольної груп співпа-дають – приймається нульова гіпотеза
(Хі-квадрат), Макномарі, Крамера-Уелча, Вілконсона-Манна-Уітні, Фішера, Стьюдента тощо). Якщо емпіричне значення критерію вияв-ляється меншим або дорівнює критичному, то можна стверджувати, що характеристики експериментальної та контрольної груп співпа-дають – приймається нульова гіпотеза  . У протилежному випадку, якщо емпіричне значення критерію виявляється більше критичного, то нульова гіпотеза не приймається, а приймається альтернативна гіпотеза – характеристики експериментальної та контрольної груп вважаються відмінними (різними) на заданому рівні значущості (тобто при тому значенні
. У протилежному випадку, якщо емпіричне значення критерію виявляється більше критичного, то нульова гіпотеза не приймається, а приймається альтернативна гіпотеза – характеристики експериментальної та контрольної груп вважаються відмінними (різними) на заданому рівні значущості (тобто при тому значенні 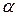 , для якого вирахувано критичне значення критерію).
, для якого вирахувано критичне значення критерію).
Не зайве вказати, що, чим менше емпіричне значення критерію (чим лівіше він знаходиться від критичного значення), тим більший ступінь співпадання характеристик контрольних та експериментальних груп (або інших груп, що порівнюються між собою). І навпаки, чим більше емпіричне значення критерію (чим правіше він знаходиться від критичного значення), тим сильніше розрізняються характеристики об’єктів, що порівнюються.
Математична статистика доводить, що теоретичний закон роз-поділу статистики критерію не залежить від результатів досліджуваних вибірок. Але цей закон розподілу може залежати від параметрів генеральних сукупностей (середніх значень, дисперсій тощо). Якщо критерій грунтується на тому чи іншому конкретному типі розподілу генеральних сукупностей або використовує параметри цих сукуп-ностей, то такий критерій називають параметричним. Параметричний критерій, таким чином, вибирається у тому випадку, коли дослідник може визначити параметри закону розподілу показника, який вив-чається. Наприклад, параметричними критеріями є широко відомі педагогічній практиці критерії, основані на 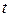 -розподілі Стьюдента і
-розподілі Стьюдента і 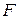 -розподілі Фішера, котрі виходять з передбачення про нормальний закон розподілу випадкових величин у генеральних сукупностях.
-розподілі Фішера, котрі виходять з передбачення про нормальний закон розподілу випадкових величин у генеральних сукупностях.
Якщо критерій не грунтується на передбаченні про конкретний тип розподілу генеральних сукупностей і не використовує параметри цих сукупностей, то його називають непараметричним критерієм.
Можливості практичного застосування параметричних і непара-метричних критеріїв суттєво залежать від характеру вимірювань характеристик досліджуваних груп. Параметричні критерії вимагають для свого застосування кількісних вимірювань (шкала інтервалів або шкала відношень). У свою чергу, непараметричні критерії використо-вують тоді, коли результати вибірок виміряні за допомогою порядкової (рангової) шкали чи шкали найменувань. Додамо, що у психолого-педагогічних дослідженнях, які володіють обмеженим набором кіль-кісних показників вимірювання змінних, саме непараметричні критерії слугують домінуючим засобом перевірки статистичних гіпотез. Крім того, їх перевагами є простота обрахунків, що буде показано у по-дальших підрозділах посібника.
Досліднику важливо прийняти рішення про використання одно-стороннього чи двостороннього критерію. Зупинимося докладніше на їхній характеристиках.
Нехай розглядаються дві (чи більше) вибірки будь-якого обсягу. Необхідно визначити величину, яка відображає відмінності характер-ристик цих вибірок. Позначимо їх через 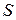 . Якщо передбачення про справедливість нульової гіпотези
. Якщо передбачення про справедливість нульової гіпотези  дозволяє встановити теоретичний закон розподілу величини
дозволяє встановити теоретичний закон розподілу величини 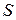 , тоді величина
, тоді величина 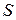 може бути використана для побудови критерію перевірки
може бути використана для побудови критерію перевірки  (статистика критерію). Вирахо-вується критерій у такій послідовності. Якщо закон розподілу статис-тики
(статистика критерію). Вирахо-вується критерій у такій послідовності. Якщо закон розподілу статис-тики 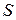 відомий, то є можливість вибрати таку частину множини усіх можливих значень
відомий, то є можливість вибрати таку частину множини усіх можливих значень 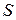 , при якій ймовірність потрапляння конкретного
, при якій ймовірність потрапляння конкретного 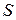 у цю зону не перевищує прийнятого рівня значущості
у цю зону не перевищує прийнятого рівня значущості 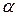 . Така частина множини усіх можливих значень статистики називається критичною зоною критерію, яка відповідє даному рівню значущості. Отже, вибір критичної зони не залежить від результатів вибірок.
. Така частина множини усіх можливих значень статистики називається критичною зоною критерію, яка відповідє даному рівню значущості. Отже, вибір критичної зони не залежить від результатів вибірок.
Таким чином, критична зона для прийнятого рівня значущості 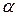 вибрана. За результатами дослідження конкретних вибірок знаходимо числове значення статистики
вибрана. За результатами дослідження конкретних вибірок знаходимо числове значення статистики 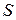 й розглядаємо два випадки (М.І. Грабар; К.А. Краснянська):
й розглядаємо два випадки (М.І. Грабар; К.А. Краснянська):
1. Знайдене значення 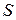 потрапило у критичну зону (здійснився розподіл, ймовірність якого не переважає рівня значущості
потрапило у критичну зону (здійснився розподіл, ймовірність якого не переважає рівня значущості 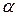 ), тобто здійснилася малоймовірна подія, яку на прийнятому рівні значущості маємо вважати невипадковою, значущою. Разом з тим підтвердження гіпотези
), тобто здійснилася малоймовірна подія, яку на прийнятому рівні значущості маємо вважати невипадковою, значущою. Разом з тим підтвердження гіпотези  означає, що відмінність результатів вибірок (що відоб-ражено у статистиці
означає, що відмінність результатів вибірок (що відоб-ражено у статистиці 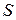 ), визначається випадковими причинами, а тому вона відхиляється й приймається альтернативна гіпотеза
), визначається випадковими причинами, а тому вона відхиляється й приймається альтернативна гіпотеза 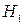 , яка стверджує, що відмінності результатів вибірок не випадкові – різниця статистично значуща.
, яка стверджує, що відмінності результатів вибірок не випадкові – різниця статистично значуща.
2. Значення Ѕ не потрапило у критичну зону. У цьому випадку дослідник не має підстав для відхилення  , нульова гіпотеза не суперечить даним спостереження, і вона приймається на даному рівні значущості.
, нульова гіпотеза не суперечить даним спостереження, і вона приймається на даному рівні значущості.
Для унаочнення викладених положень використаємо графічне зображення критичних зон одностороннього та двостороннього типів (Рис. 8.2; 8.3; 8.4)
|
|
|
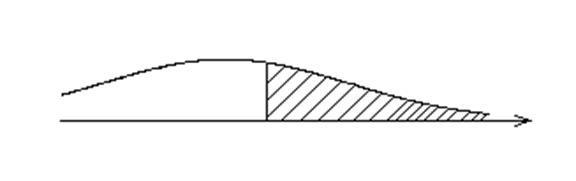
Рис.8.2. Критична зона одностороннього типу (випадок І)
|
|
|

Рис.8.3. Критична зона одностороннього типу (випадок ІІ)
|
|
|
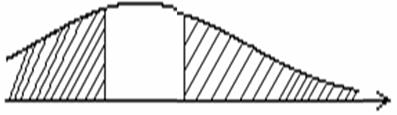
Рис.8.4. Критична зона двостороннього типу
Зауважимо, що двостороння критична зона (рис. 3) може бути утворена шляхом об’єднання односторонніх критичних зон, які відповідають рівню значущості 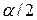 .
.
Використовуючи критичні зони одностороннього та двосто-роннього типу, слід формулювати правило для відхилення нульової гіпотези таким чином: якщо використовується одностороння зона І випадку (рис.1), то нульова гіпотеза  відхиляється тоді, коли
відхиляється тоді, коли 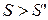 ; при використанні односторонньої зони ІІ випадку відхилення нульової гіпотези настає при
; при використанні односторонньої зони ІІ випадку відхилення нульової гіпотези настає при 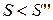 . Нарешті, у випадку двосторонньої критич-ної зони
. Нарешті, у випадку двосторонньої критич-ної зони  відхиляється, якщо справедливою є нерівність:
відхиляється, якщо справедливою є нерівність: 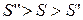 .
.
Отже, якщо використовуємо односторонню критичну зону, то вибираємо односторонній критерій перевірки досліджуваних розподілів; і, навпаки,– двосторонній критерій застосовуємо тоді, коли маємо двосторонню критичну зону розподілу.
Для педагогічної практики важливим є підхід до вибору одно-стороннього чи двостороннього критерію за А.Т. Ашеровим. Він вказує, що якщо у дослідника немає підстав передбачати, що, наприклад, оцінки студентів контрольної групи в середньому суттєво відрізняю-ться від оцінок студентів експериментальної групи, тоді приймається двосторонній критерій (закони розподілу випадкових величин 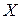 і
і 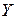 однакові); при умові, що у дослідника є підстави передбачати, що оцінки студентів контрольної групи в середньому суттєво відрізняються від оцінок студентів експериментальної групи, то приймається одно-сторонній критерій (закони розподілу випадкових величин
однакові); при умові, що у дослідника є підстави передбачати, що оцінки студентів контрольної групи в середньому суттєво відрізняються від оцінок студентів експериментальної групи, то приймається одно-сторонній критерій (закони розподілу випадкових величин 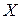 і
і 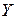 різні).
різні).
Дата добавления: 2015-11-06; просмотров: 3132;