Статистичних гіпотез

На вибір методів перевірки статистичних гіпотез впливає декілька факторів. Наприклад, важливо врахувати, за якою шкалою виміряні властивості учасників педагогічного експерименту. Нагадаємо, що при використанні шкали найменувань, досліджувані об’єкти розподі-ляються на декілька класів. Дані, отримані за цією шкалою, дозволяють відповісти на питання: «Володіє чи не володіє досліджуваний об’єкт певною якістю?» Якщо дослідник має дані, отримані на рівні порядкової шкали, то ця інформація є більш повною для аналізу. У порівнянні зі шкалою найменувань, отримані дані за порядковою шкалою додатково дозволяють вияснити, у якого з двох об’єктів досліджувана властивість виражена сильніше.

Шкала відношень, у свою чергу, більш інформативна у порів-нянні зі шкалою порядку. Дані, отримані за цією шкалою, дозволяють досліднику вияснити, у скільки разів чи на скільки одиниць власти-вість, що вимірюється, більша у одного з двох об’єктів. Додамо, що у сучасних науково-педагогічних дослідженнях найчастіше використо-вують порядкову шкалу або шкалу відношень.

Крім того, досліднику слід враховувати число значень, що відрізняються між собою у вибірках. Наприклад, вибірка 1; 2; 2; 2; 1; 1; 2; 1; 2; 1 має лише два різних значення – одиниця і двійка. А вже вибірка виду 3; 1; 4; 2; 9; 0; 8; 6; 5; 7 має десять різних значень. Важливим фактором вибору методу перевірки статистичних гіпотез є характеристика вибірки. Вибірка, насамперед, може бути залежною і незалежною. Якщо у констатувальному й формувальному експерименті беруть участь одні й ті самі студенти, така вибірка вважається залеж-ною. Природно, перевірку однорідності контрольних та експеримен-тальних груп не проводять. І, навпаки, якщо у констатувальному й формувальному експерименті беруть участь студенти різних груп, такі вибірки називають незалежними. Крім того, необхідно враховувати кількість студентів (об’єм вибірки), які беруть участь у експерименті. Д.А. Новіков пропонує вживати дві характеристики: об’єм вибірки великий ( 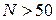); об’єм вибірки малий ( 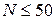). Додамо, що наведені межі поділу є досить умовними, приблизними. Наприкінець зазначимо, що на вибір способу перевірки статистичних гіпотез суттєвий вплив має можливість експериментатора зробити припущення щодо харакреру розподілу (див. параметричні й непараметричні критерії). Якщо можна зробити припущення щодо характеру розподілу даних, що аналі-зуються, то такі методи називають параметричними. До іншої групи належать методи, при використанні яких не роблять припущень щодо теоретичного закону розподілу даних (непараметричні методи). Розгля-немо умови застосування деяких статистичних критеріїв, користуючись відповідними логічними схемами (рис. 8.5; 8.6).

Критерій Макномарі. Критерій призначено для порівняння роз-поділів об’єктів двох сукупностей на основі вимірювання будь-якої властивості (навіть за шкалою найменувань) у двох залежних вибірках.

Для застосування Критерію Макномері необхідно дотримуватися таких вимог:

- вибірки випадкові (сформовані методи випадкового відбору);

- вибірки залежні (наприклад, двократне вимірювання якоїсь властивості у членів однієї й тієї ж групи до та після експеримен-тальної ситуації);

- пари ( 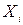, 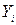) взаємно незалежні, тобто члени вибірки не впли-вають один на одного;

- шкала вимірювання – шкала найменувань (вище – нижче, більше – менше, так – ні, згоден – незгоден) з 2 категоріями.

Критерій Стьюдента. Перевірка достовірності результатів педаго-гічного експерименту за критерієм Стьюдента ( 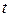-критерій) проводиться за таких умов:

- вибірки взяті з генеральних сукупностей з нормальним законом розподілу й мають однакові стандартні відхилення;

- необхідно визначити при порівнянні середніх балів експери-ментальних і контрольних груп не тільки у якій групі середній бал вище, а й на скільки вище.

Критерій Пірсона ( 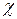-квадрат). Критерій 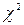застосовується для порівняння об’єктів двох сукупностей за станом певної властивості, на основі вимірювання за шкалою найменувань у двох незалежних вибірках.

Вимоги до застосування критерію :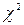

- вибірки випадкові;

- вибірки незалежні, члени кожної вибірки також незалежні між собою (наприклад, маємо контрольний та експериментальний масив і виміри виконуємо до і після введення педагогічної інновації);

- сума обсягів двох вибірок ( 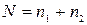) більше 20;

- жодна з абсолютних частот, визначених на основі експеримен-тальних даних, не може бути менше 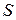(наприклад, при групуванні студентів контрольних та експериментальних груп за ставленням до нового методу навчання (шкала найменувань, відповіді «так» і «ні»), кожна із чотирьох підгруп студентів має становити не менше 5 осіб!). У випадку, якщо в одну категорію потрапить менше 5 осіб, варто об’єднати дві суміжні категорії, щоб задовольнити означену вимогу. Наприклад, якщо є п’ять категорій студентів із диференціацією рівнів сформованості якоїсь властивості: «високий», «середній», «нижче середнього», «низький», «дуже низький» і респонденти розподілилися відповідно 10; 18; 15; 7; 1; то варто відмовитися від категорії «дуже низький» і об’єднати її з категорією «низький», отримавши дані за цим групуванням 8 осіб;

- якщо властивість об’єктів, яка вивчається, виміряна за шкалою найменувань, яка має більше двох категорій, або за шкалою більш високого рівня, то для порівняння розподілів цієї властивості в різних сукупностях слід використовувати лише двосторонній критерій Х².

Критерій Вілконсона-Манна-Уітні. Цей критерій (ВМУ) призна-чений для визначення відмінностей у розподілах властивості, що вивчається у об’єктів двох сукупностей на основі порівняння резу-льтатів у членів незалежних вибірок. За допомогою критерію ВМУ перевіряється одночасно передбачення про відмінність як медіан, так і середніх значень у досліджуваних сукупностях.

Застосування критерію ВМУ можливе при дотриманні таких вимог:

- обидві вибірки випадкові;

- вибірки незалежні, члени кожної вибірки також незалежні між собою;

- властивість, що вивчається, в об’єктах має неперервний характер в обох сукупностях, з яких зроблено вибірки;

- шкала вимірювання не нижча порядкової;

- оскільки критерій ВМУ оперує не з абсолютними значеннями елементів двох вибірок, а з результатами їх парних порівнянь, то він дає недостатньо точні дані в умовах, коли число значень, які відріз-няються одне від одного, у вибірках невелике.

Рис. 8.5. Логічна схема вибору критерію для перевірки статистичної гіпотези про однорідність контрольної

Рис. 8.6. Алгоритм вибору статистичного критерію

(за Д.А. Новіковим)