Визначення статистичних характеристик даних вибірки спостережень.
Генеральна сукупність — множина однотипних об’єктів, кіль-
кісна чи якісна ознака яких підлягає вивченню.
Вибіркова сукупність — підмножина об’єктів, дібраних у відповідний спосіб із генеральної сукупності. Вважаємо, що ознака, яка вивчається, є випадковою величиною Х із функцією розподілу 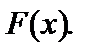
Результати вибірки розглядатимемо як послідов-
ність незалежних однаково розподілених випадкових величин 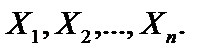 Закон розподілу для всіх
Закон розподілу для всіх 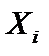 визначається функцією
визначається функцією 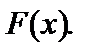
Результати вибірки — реалізації випадкових вели-
чин — позначатимемо відповідно через 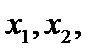
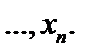 Розмістивши ці числа в порядку зростання і записавши частоти
Розмістивши ці числа в порядку зростання і записавши частоти 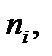 з якими зустрічаються ці значення, дістанемо варіаційний, або статистичний, ряд:
з якими зустрічаються ці значення, дістанемо варіаційний, або статистичний, ряд:
| xi | x1 | x2 | … | xk |
| Частоти | n1 | n2 | … | nk |
На підставі такого ряду можна побудувати статистичну функцію розподілу 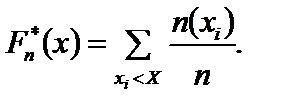 Якщо
Якщо 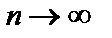 , то статистична функція розподілу збігається до теоретичної функції розподілу.
, то статистична функція розподілу збігається до теоретичної функції розподілу.
Статистичний ряд графічно подається полігоном розподілу. Щоб побудувати його, на осі абсцис відкладають значення реалізацій, а на осі ординат — відповідні їм частоти (відносні частоти). Здобуті точки сполучають відрізками прямих.
У разі, коли Х — неперервна величина і обсяг вибірки великий, результати вибірки подають інтервальним рядом. Для цього область реалізацій розбивають на k інтервалів і для кожного інтервалу визначають частоти. Кількість інтервалів 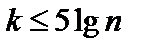 , а їхню довжину
, а їхню довжину 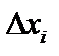 найчастіше беруть однаковою. Здобутий ряд геометрично подається гістограмою. Для побудови її на осі абсцис відкладають інтервали, а на них як на основах будують прямокутники, висота яких пропорційна до частоти (відносної частоти) інтервалу. Гістограма дає певне уявлення про графік щільності розподілу.
найчастіше беруть однаковою. Здобутий ряд геометрично подається гістограмою. Для побудови її на осі абсцис відкладають інтервали, а на них як на основах будують прямокутники, висота яких пропорційна до частоти (відносної частоти) інтервалу. Гістограма дає певне уявлення про графік щільності розподілу.


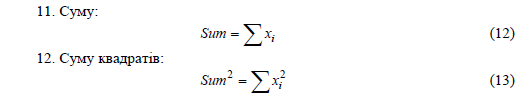
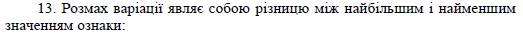

Дата добавления: 2015-11-20; просмотров: 1184;
