Незалежно від проблем, що вивчаються , кожне наукове дослідження ставить перед собою задачу підтвердити чи відкинути якусь гіпотезу.
Перевірка статистичних гіпотез
Статистичні гіпотези - це припущення, котрі відносяться до виду розподілу випадкової величини або окремих його параметрів.
Задача випробування статистичних гіпотез виникає тоді, коли обставини вимушують нас робити вибір між двома способами дії.
Гіпотеза, прийнята дослідником, називається нульовою гіпотезою (Н0). Протилежна гіпотеза називається альтернативною (Н1).
Наприклад, якщо вивчаються властивості профілактичної сироватки, може бути прийняте припущення, що ця сироватка таких властивостей не має або вони не відрізняються від аналогів. Це нульова гіпотеза. Альтернативною гіпотезою у цьому випадку буде твердження, що сироватка має профілактичні властивості кращі ніж в аналогів. Можна поміняти гіпотези місцями і це не змінить постановку експерименту, метою якого є перевірка властивостей сироватки.
Серед розмаїття задач, які розв'язуються за допомогою методів математичної статистики, в медицині найчастіше трапляються задачі пов’язані з характеристикою окремої сукупності або пов’язані з порівнянням двох сукупностей між собою.
Якщо розглядається окрема сукупність, то нульова гіпотеза Н0 формулюється у вигляді – досліджувана сукупність підлягає певному відомому розподілу, напр. нормальному.
Якщо порівнюються дві сукупності, то нульова гіпотеза переважно має вигляд: не існує достовірних відмінностей між двома групами показників, тобто дві групи належать до однієї сукупності.
Для перевірки гіпотез використовують статистичний критерій K – це вирішуюче правило, яке забезпечує прийняття вірної гіпотези і відхилення хибної з великою ймовірністю. Математичною основою будь-якого критерію є статистична характеристика, закон розподілу якої відомий, наприклад, характеристика t – розподілу Стьюдента.
Ймовірність з якою може бути відхилена нульова гіпотеза, коли вона є вірною, називається рівнем значущості. Рівень значущості дослідник вибирає в залежності від особливостей об'єкта дослідження. Для більшості медичних статистичних розрахунків приймається, що максимальний рівень значущості, при якому нульову гіпотезу відхиляють, має дорівнювати 0,05. Але в особливо важливих випадках, наприклад, якщо дослідження пов'язані з використанням токсичних засобів чи інших факторів високого ризику, рівень значущості приймається рівним 0,01.
Сукупність значень, при яких основна гіпотеза не приймається називається критичною областю. Точки, що відділяють критичну область від області прийняття рішень називаються критичними. Для визначення критичної області задається рівень значущості α. Для кожного з критеріїв є таблиці, за якими знаходять значення критичних точок.
Задача найкращого вибору критичної області розв’язується звичайно так, щоб критерій перевірки мав найбільшу чутливість, тобто щоб ми мали найбільшу ймовірність попадання нашого критерію в критичну область, коли вірна альтернативна гіпотеза. Ця ймовірність носить назву міцності критерію.
При аналізі гіпотез можливі помилки двох видів:
· Н0 відкидається, коли вона правильна – помилка I-го роду
· Н0 приймається, коли правильна Н1 – помилка II-го роду
Знижуючи рівень значущості ми зменшуємо ймовірність помилки першого роду, але при цьому зростає ймовірність помилки другого роду.
Критерії бувають однобічні і двосторонні
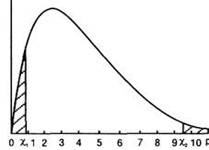 |
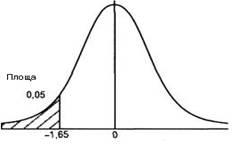
У випадку, коли H1 сформульована у виді θ ≠ θ0, використовується двосторонній критерій (рис. 7).
Рис.7. Приклад критичної області для двостороннього і однобічного критерію
Якщо ж ми формулюємо Н1, у виді θ < θ0 (чи θ > θ0), то в цьому випадку використовується однобічний критерій (рис. 7).
Перевірка гіпотез звичайно проходить наступні етапи.
1. Визначення статистичної моделі. Тут висувають деякий набір передумов щодо закону розподілу випадкової величини і його параметрів. Наприклад, закон розподілу нормальний, величини незалежні й ін.
2. Формулюють Н0 і Н1.
3. Вибирають критерій (критеріальну статистику), що підходить до висунутої статистичної моделі.
4. Вибирають рівень значущості a залежно від необхідної надійності висновків.
5. Визначають критичну область для перевірки Н0.
6. Розраховують значення обраного статистичного критерію для наявних даних.
7. Розраховане значення критерію порівнюють із критичним. і потім вирішують прийняти чи відхилити Н0.
Перевірка статистичних гіпотез здійснюється з допомогою різних статистичних критеріїв: параметричних або непараметричних. При виборі критерію, крім інших умов, необхідно враховувати чи вибіркові сукупності є зв’язаними чи незалежними. Прикладами перших сукупностей є вибірки з попарно зв’язаними варіантами (кількість гемоглобіну в крові пацієнтів до і після лікування, різні фізіологічні показники спортсменів до і після старту). Сукупності другого роду не зв’язані між собою і можуть мати різні обсяги (результати дослідження крові в декількох груп хворих з різними стадіями захворювання, результати дослідження піддослідної та контрольної груп тварин)
При виборі критерію необхідно завжди виходити з прикладної постановки задачі і природи даних.
Дата добавления: 2015-10-21; просмотров: 686;
