Коефіцієнт парної кореляції
Коефіцієнт парної кореляції обчислюється за формулою:
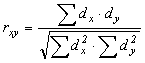 або
або 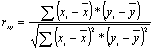
Алгоритм розрахунку коефіцієнта парної кореляції:
1) записують вихідні дані в два варіаційні ряди - x і y;
2) обчислюють середнє арифметичне ряду x і y;
3) визначають різницю між членом ряду і середніми величинами;
4) перемножують різниці ряду x і y між собою;
5) знаходять суму перемножуваних різниць (з урахуванням арифметичного знаку);
6) зводять квадрат кожної різниці (відхилення) ряду х і у;
7) визначають суму квадратів відхилень (різниць) для ряду х і окремо;
8) підставляють отримані дані у вихідну формулу і обчислюють коефіцієнт парної кореляції.
Приклад. Визначити кореляційний зв'язок між рядками введення протидифтерійної сироватки та летальністю цього захворювання.
| День введення сироватки (х) | Летальність (у) | d x | d y | d x 2 | d y 2 | d x * d x |
| 1-й | 2,0 | -2 | -5 | |||
| 2-й | 3,0 | -1 | -4 | |||
| Третя | 7,0 | |||||
| 4-й | 9,0 | +1 | +2 | |||
| 5-й | 14,0 | +2 | +7 | |||
| x x = 3 | x y = 7.0 | Sd x = 0 
| Sd y = 0 
| Sd x 2 = 10 
| Sd y 2 = 94 
| Sd x * d y = 30 
|
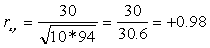
Коефіцієнт кореляції дорівнює +0,98. Зв'язок позитивна, сильна. Отже, між термінами введення сироватки та летальністю від дифтерії є дуже тісна залежність. Число хворих у цьому прикладі дорівнює 900.
Можна визначити достовірність коефіцієнта кореляції, обчисливши його середню помилку для великого числа спостережень (n> 50) за формулою:
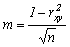 , Або при меншій кількості спостережень:
, Або при меншій кількості спостережень: 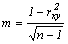
З достатньо великою надійністю можна стверджувати, що залежність невипадкова, якщо чисельне значення r xy перевищує свою середню помилку не менш ніж в 3 рази.
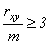
Тобто зв'язок між ознаками вважається статистично значущим, якщо коефіцієнт кореляції перевищує свою помилку в 3 і більше разів.
У тому випадку, коли відношення коефіцієнта кореляції до його середньої помилки менше 3, існування зв'язку між досліджуваними явищами не можна визнати доведеним.
Для малої кількості спостережень (n £ 30) ступінь надійності коефіцієнта кореляції може визначатися за спеціальною таблицею. При цьому число спостережень таблиці К (число ступенів свободи n ) дорівнює кількості спостережень у дослідженні без двох, тобто К = n-2. Як правило, коефіцієнт кореляції розраховується при числі кореляційних пар не менше 5.
У медичних і біологічних дослідженнях зв'язок між ознаками вважається статистично значущим, якщо величина коефіцієнта кореляції більше або дорівнює табличній при Р = 0,05
Показники оцінки коефіцієнта кореляції при малому числі спостережень
| K | P | |||
| 0,1 | 0,05 | 0,02 | 0,01 | |
| 0,988 | 0,997 | 0,9995 | 0,99988 | |
Приклад. У районах вивчалася залежність між щепленнями населення і рівнем захворюваності. Отриманий коефіцієнт кореляції за цими двома ознаками дорівнював 0,81. Число спостережень - 8 районів (пар), отже, К дорівнює 6 (8-2). По таблиці знаходимо рядок 6 і порівнюємо отриманий коефіцієнт. При даному числі ступенів свободи (К) коефіцієнт кореляції перевищує табличний для ймовірності Р = 0,05 (графа 3). Звідси з ймовірністю, більшою, ніж 95%, можна стверджувати, що залежність між щепленнями населення і захворюваністю не випадкова, і цей зв'язок сильна, тобто чим більше відсоток щеплених, тим менше рівень захворюваності.
Ранговий коефіцієнт (Спірмена)
Ранговий коефіцієнт кореляції більш придатний в порівнянні зі звичайним коефіцієнтом для характеристики кореляцій у випадках нелінійної зв'язку і для даних, розподіл яких відрізняється від нормального. Крім того, дані для розрахунку рангового коефіцієнта можуть бути представлені в напівкількісних вимірах. Обчислення коефіцієнта проводиться за формулою:
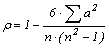
Алгоритм розрахунку коефіцієнта кореляції рангів:
1) замінюють кількісні (або напівкількісні, або якісні) ознаки ряду х і у на ранги, ранжуючи при цьому строго від меншої величини до більшої (або суворо від більшої до меншої на розсуд дослідника);
2) визначають умовні відхилення (а), тобто різницю рангів по кожному рядку;
3) зводять умовні відхилення в квадрат;
4) визначають суму квадратів умовних відхилень;
5) підставляють отримані дані у відому формулу і обчислюють коефіцієнт кореляції.
Приклад. Виміряти кореляцію між смертністю від раку молочної залози і раку матки (матеріали смертності 5 позаєвропейських країн за 1950 - 1952 рр..),
| Країна | Смертність від раку молочної залози на 100000 жінок х | Смертність від раку матки на 100000 жінок у | Порядкові номери (ранги) за розмірами смертності від раку | Різниця рангів а | Квадрат різниці рангів а 2 | |
| молочної залози | матки | |||||
| Нова Зеландія | 28,6 | 14,9 | ||||
| Австралія | 23,5 | 13,4 | ||||
| ПАР | 21,1 | 16,3 | ||||
| Чилі | 5,8 | 15,3 | ||||
| Японія | 3,3 | 19,1 | ||||
| Sа 2 = 36 |
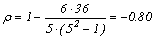
Оскільки обчислення коефіцієнта кореляції рангів зазвичай проводиться на малій кількості числі спостережень (кількість пар в лавах х, у), особливого значення набуває оцінка статистичної значущості (достовірності) цього коефіцієнта. Ранговий коефіцієнт завжди менш точний, ніж парний коефіцієнт кореляції.
Оцінка достовірності коефіцієнта кореляції рангів проводиться різними методами в залежності від числа спостережень. При числі парних спостережень, меншому за число 9 (n £ 9), оцінка значимості проводиться за спеціальною таблицею. При числі спостережень від 10 і більше оцінка значимості може здійснюватися за допомогою критерію t за формулою:
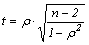 .
.
Використовуючи таблицю значень t Стьюдента, при числі ступенів свободи без двох (n2= n-2), порівнюють обчислене значення з табличним. Коефіцієнт визнається значущим за умови, якщо розрахункове t> t0,05 табличного.
Критичне значення коефіцієнтів кореляції Спірмена - r
| n | Рівні значущості | n | Рівні значущості | ||
| 5% | 1% | 5% | 1% | ||
| 1,000 | 0,425 | 0,601 | |||
| 0,900 | 1,000 | 0,399 | 0,564 | ||
| 0,829 | 0,843 | 0,377 | 0,534 | ||
| 0,714 | 0,893 | 0,359 | 0,508 | ||
| 0,643 | 0,833 | 0,343 | 0,485 | ||
| 0,600 | 0,783 | 0,329 | 0,465 | ||
| 0,564 | 0,746 | 0,317 | 0,448 | ||
| 0,506 | 0,712 | 0,306 | 0,435 | ||
| 0,456 | 0,645 |
Коефіцієнт кореляції визнається значущим (достовірним), якщо обчислене r £ r 0,05.
У розглянутому прикладі число спостережень менше 9 (n = 5), внаслідок чого оцінка коефіцієнта проведена за таблицею. При числі спостережень, що дорівнює 5, розраховане значення r =- 0,80 менше критичного і тому не можна з достатньою вірогідністю стверджувати, що між смертністю від раку молочної залози і раку матки існує якась залежність.
Визначення тісноти зв'язку між якісними ознаками
При вивченні залежності якісних ознак використовується коефіцієнт спряженості. Для визначення тісноти зв'язку в разі альтернативної залежності двох ознак , які співставляються (дані, як правило, представлені в таблицях з чотирма полями) коефіцієнти спряженості розраховуються за формулами:
коефіцієнт контингенции Шарльє:
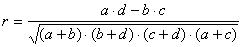
коефіцієнт асоціації Юла (Q):
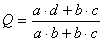
Алгоритм розрахунку:
1) шифрують через a, b, c, d чотири поля, в яких розташовані вихідні дані: 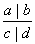 ;
;
2) обчислюють послідовно твори a * d і b * c;
3) розраховують чисельник формули;
4) визначають знаменник формули;
5) обчислюють коефіцієнт Шарльє або Юла.
Приклад. Визначити залежність між методами лікування (хірургічний і рентгенотерапія, тільки хірургічний) і результатами (одужання чи неодужання).
| Метод | Одужання | Неодужання | Усього хворих |
| I | 14 (a) | 8 (b) | 22 (a + b) |
| II | 7 (c) | 9 (d) | 16 (c + d) |
| Усього: | 21 (a + c) | 17 (b + d) | 38 (a + b + c + d) = N |
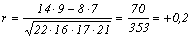
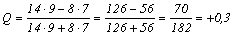 .
.
Примітка. Коефіцієнт асоціації дає швидку, але орієнтовну оцінку зв'язку. Досить точну величину коефіцієнт Q визначає для значень r між 1,5 і 0,5.
У тих випадках, коли якісні фактори мають не альтернативне варіювання (чотири поля), а більше число угруповань, коефіцієнт спряженості обчислюється за формулою:
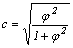 ,
,
де j 2 (фі-квадрат) - коефіцієнт контингенції Пірсона.
Алгоритм розрахунку:
1) встановлюють кореляційну таблицю;
2) частоти (числа спостережень) вписують зверху кожної клітини таблиці;
3) частоти зводять у квадрат і результат записують під ними;
4) квадрат частот ділять на суму числа спостережень (частот) кожної графи таблиці (див. приклад розрахунку: 625:46 = 12,7; 225:75 = 3 і т.д.);
5) результат від ділення проставляють внизу кожної клітини таблиці;
6) визначають суму результату від ділення по кожному рядку і записують у нижній частині підсумкової клітини таблиці (12,7 +3,0 +2,0 = 17,7 і т.д.);
7) зазначені суми ділять на відповідні підсумки рядків (сума від числа спостережень за рядком): 17,7:50 = 0,35; 24,5:60 = 0,4 і т.д.;
8) обчислюють значення j 2, який є сумою отриманих вище результатів від ділення без одиниці (j 2 = 1,28-1 = 0,28);
9) отримане значення j 2 підставляють у формулу і обчислюють коефіцієнт спряженості С.
Приклад. Обчислити коефіцієнт спряженості при вимірюванні тісноти зв'язку між житловими умовами і захворюваністю обстежуваних.
| Житлові умови | Розподіл обстежуваних за частотою захворювань | Разом | |||
| Частота хворіють | Епізодично хворіють | Чи не хворіють | |||
| Незадовільні | |||||
| 25 2 = 625 | |||||
| 12,7 | 17,7 | 0,35 | |||
| Задовільні | |||||
| 6,6 | 17,3 | 0,6 | 24,5 | 0,4 | |
| Хороші | |||||
| 0,8 | 7,7 | 28,6 | 37,1 | 0,53 | |
| 25 +18 +6 = 49 | 0,35 +0,4 +0,53 = 1,28 |
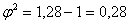 , Звідси
, Звідси 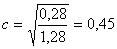 .
.
Величина С дозволяє судити про наявність середнього кореляційного зв'язку між розглянутими факторами.
Дата добавления: 2015-10-21; просмотров: 1754;
