Приклад перевірки однорідності незалежних вибірок
за критерієм 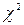 (Хі– квадрат)
(Хі– квадрат)
Проводився експеримент, спрямований на визначення ефектив-ності з двох методик підготовки та проведення лекцій. Експеримент проходив у двох групах студентів (вибірка № 1, контрольна група, 101 особа; вибірка № 2, експериментальна група, 100 осіб). У конт-рольній групі лекційні заняття проводилися традиційно: викладач проводив пояснювально-ілюстративні лекції, а студенти усталено вибудовували конспект на занятті, який і був, переважно, основним джерелом інформації щодо оволодіння курсом.
На іншому потоці (експериментальна група) лекційні заняття проводилися з використанням принципу обов’язкової підготовки сту-дента до лекції: кожен мав наперед розробити конспект (власний!), а на занятті законспектувати поряд з домашніми записами поданий проблемним методом навчальний матеріал та наприкінці зробити висновки.
На завершення вивчення курсу обома потоками студентів шляхом експертної оцінки було визначено рівень навчально-пізнавальної діяльності студентів (репродуктивний; перехідний; творчий). Зважаючи на те, що вибірки випадкові й незалежні, на початку експерименту визначені як однорідні, передбачалося перевірити гіпотезу про від-сутність відмінностей обох методик підготовки та проведення лекційних занять (  ). Додамо, що результати виміряно за допомогою поряд-кової шкали, яка має три категорії. Отже, виконуються умови засто-сування критерію
). Додамо, що результати виміряно за допомогою поряд-кової шкали, яка має три категорії. Отже, виконуються умови засто-сування критерію 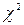 (Хі – квадрат, критерію Пірсона) для перевірки сформульованої гіпотези. Результати експерименту оформляємо у вигляді таблиці 8.17, де позначаємо відповідні комірки емпіричних частот (1А; 2Б4 3В тощо). Для розрахунку критерію
(Хі – квадрат, критерію Пірсона) для перевірки сформульованої гіпотези. Результати експерименту оформляємо у вигляді таблиці 8.17, де позначаємо відповідні комірки емпіричних частот (1А; 2Б4 3В тощо). Для розрахунку критерію 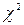 дані табл. 8.17 заносимо у таблицю 8.18. При цьому у стовпчику 2 табл. 8.18 записуємо емпіричні частоти; у стовпчик 3 записуємо очікувані (теоретичні) частоти. Для знаходження теоретичної частоти в будь-якій клітинці таблиці необхідно перемножити відповідні маргинальні частоти й розділити добуток на суму. Наприклад, очікувана (теоре-тична) частота для комірки А дорівнює 29, 10. Послідовно заповнюємо стовпчики 4, 5 і 6 табл. 8.18, виконуючи арифметичні дії з відпо-відними емпіричними та теоретичними частотами. Сума чисел 6 стовпчика у нашому прикладі дорівнює 8,53. Це і є емпіричне значення критерію
дані табл. 8.17 заносимо у таблицю 8.18. При цьому у стовпчику 2 табл. 8.18 записуємо емпіричні частоти; у стовпчик 3 записуємо очікувані (теоретичні) частоти. Для знаходження теоретичної частоти в будь-якій клітинці таблиці необхідно перемножити відповідні маргинальні частоти й розділити добуток на суму. Наприклад, очікувана (теоре-тична) частота для комірки А дорівнює 29, 10. Послідовно заповнюємо стовпчики 4, 5 і 6 табл. 8.18, виконуючи арифметичні дії з відпо-відними емпіричними та теоретичними частотами. Сума чисел 6 стовпчика у нашому прикладі дорівнює 8,53. Це і є емпіричне значення критерію 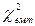 .
.
Таблиця 8.17
Емпіричні частоти критерію 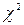 для студентів контрольної та експериментальної груп (дані умовні)
для студентів контрольної та експериментальної груп (дані умовні)
| Рівні навчально-пізнавальної діяльності студентів | Емпіричні частоти | Всього | |
| Контрольна група | Експериментальна група | ||
| Репродуктивний | 38 (А) | 20 (Б) | |
| Перехідний | 45 (В) | 51 (Г) | |
| Творчий | 18 (Д) | 29 (Е) | |
| Всього |
Таблиця 8.18
Дата добавления: 2015-11-06; просмотров: 931;
