Розподіл часу самостійної підготовки студентів до модульної контрольної роботи та успішності засвоєння модуля
| № респон-дента | Самостійна підготовка до контрольної роботи ( 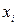 ), год. ), год.
| Резуль-тати тестува-ння,
( 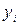 ) бали ) бали
| 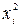
| 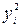
| 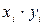
|
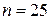
|
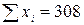
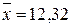
|
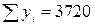 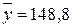
|
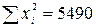
|
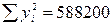
| 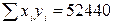
|
Приклад 3. За даними таблиці 8.11 вияснимо, на скільки пов’язані мотиви навчання студентів 1-го курсу агрономічного та юридичного факультетів аграрного університету. Зауважимо, що соціально-демо-графічні характеристики студентів факультетів суттєво відрізняються. Для цього пропонуємо значення відсоткових розподілів для кожної з двої груп (дані умовні).
Таблиця 8.11
Результати дослідження мотивації навчання студентів агрономічного та юридичного факультетів (1 курс) аграрного університету*
| №п/п | Мотиви навчання | Факультет % | Ранги І | Ранги ІІ | 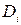
| 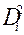
| |
| Агроно-мічний | Юридич- ний | ||||||
| Учусь, щоб у майбутньому покращити добробут села | 57,5 | 50,9 | 3,5 | -2,5 | 6,25 | ||
| Учусь заради вищої освіти як критерію працевлаштування | 57,3 | 61,2 | |||||
| Майбутня робота за фахом розв’яже мої матеріальні проблеми | 53,8 | 54,2 | |||||
| Учусь заради престижу вищої освіти, хочу ствердитися в очах друзів і знайомих | 49,7 | 50,9 | 3,5 | 0,5 | 0,25 | ||
| Учусь, бо є потреба в оволодінні новими знаннями, інтерес до знань | 48,6 | 51,4 | |||||
| Хочу в майбутньому бути корисним суспільству | 43,0 | 40,3 | |||||
| Учусь виключно на вимогу рідних | 21,3 | 18,3 | |||||
| Усі зараз здобувають освіту, і я навчаюсь, аби навчатися | 9,8 | 7,2 | |||||
| Всього | 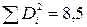
|
*У таблиці розподіл студентів юридичного та агрономічного факультетів за мотивами навчання подано у відсотках. Через те, що респонденти могли вибрати більше одного мотиву навчання, сума стовпчиків не дорівнює 100%.
Оскільки обидві змінні вимірюються у шкалах порядка (рангова шкала), то як міру зв’язку використаємо коефіцієнт рангової кореляції Спірмена. Він вираховується за формулою:
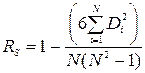 , (10)
, (10)
де 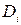 – різниця між іншими парами рангів;
– різниця між іншими парами рангів;
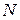 – число пар рангів, що зіставляються.
– число пар рангів, що зіставляються.
Зупинимося на особливостях заповнення таблиці 11. У графі таблиці «юридичний факультет» зустрічаються два однакових числа (50,9). У таких випадках обом числам присвоюється ранг, рівний середньому арифметичному з рангів, які б вони зайняли (3 і 4):
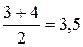 .
.
Практика показує, що ця операція викликає певні труднощі у дослідників, а тому доцільно доповнити цей матеріал таким уявним прикладом: експерт при ранжуванні певних об’єктів отримав розподіл: 1; 1; 1; 2; 3; 4; 5; 6. Як бачимо, на перше місце поставлено 3 об’єкти. Значить ці об’єкти зайняли 1, 2 і 3 місця в ранжованому ряді. Тому знаходимо суму 1+2+3=6, ділимо її на 3 і присвоюємо зазначеним об’єктам один ранг “2”.Тоді ряд буде мати такий вигляд: 2; 2; 2; 4; 5; 6; 7; 8. Щоб перевірити правильність дій, варто знайти суму усіх рангів. Якщо ранжують 8 об’єктів, то їх сума у будь-якому випадку (незалежно від того, були «зв’язані» ранги чи ні) повинна дорів-нювати 36. Звісно, якщо ранжованих об’єктів 9, то ця сума буде дорівнювати 45; 10 – 55; 11 – 66 і т.д.
Підставимо величини, вирахувані в таблиці 11 у формулу (10):
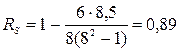
Таку величину коефіцієнта кореляції можна інтерпретувати як високу ступінь зв’язку між мотивами навчання студентів двох різних факультетів – агрономічного та юридичного. Але, разом з тим, така величина коефіцієнта кореляції не повинна ввести в оману дослідника: мотиви навчання студентів обох факультетів чітко розподіляються на дві групи. За першими чотирма мотивами єдності думок респондентів не спостерігається. А для іншої групи мотивів (5; 6; 7; 8) ранги повністю співпадають. Отже, крім визначення величини коефіцієнта рангової кореляції, обробку даних експерименту слід доповнити якісним аналізом таблиці 11.
Розглянувши приклади визначення коефіцієнта кореляції, зупини-мося на аспектах статистичної значущості цього показника. Іншими словами, треба дати відповідь на питання: «Чи не обумовлена за-лежність, яку він фіксує, випадковими відхиленнями?» (перевіряється гіпотеза того, що отримані дані «суттєво» відрізняються від 0).
Якщо гіпотезу  (
( 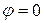 ), буде відхилено, стверджують, що величина коефіцієнта кореляції статистично значуща (ця величина не обумовлена випадковістю) при рівні значущості
), буде відхилено, стверджують, що величина коефіцієнта кореляції статистично значуща (ця величина не обумовлена випадковістю) при рівні значущості 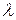 .
.
Розглянемо процедуру перевірки статистичної значущості коефі-цієнта кореляції Пірсона.
1 випадок. Коли число респондентів 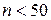 , застосовується кри-терій розподілу Стьюдента
, застосовується кри-терій розподілу Стьюдента 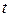 , який вираховується за формулою:
, який вираховується за формулою:
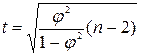 (11)
(11)
За таблицями критичних значень для 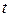 – розподілу Стьюдента знаходимо
– розподілу Стьюдента знаходимо 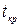 відповідно числа ступенів свободи
відповідно числа ступенів свободи 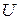 , яке вираховується за формулою:
, яке вираховується за формулою:
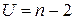 ,
,
де 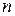 – кількість респондентів.
– кількість респондентів.
Вибираємо рівень значущості (переважно, не більше 0,05) і порівнюємо розраховане і критичне значення критерію 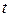 . Якщо для рівня значущості
. Якщо для рівня значущості 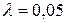
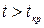 , маємо констатувати, що коефіцієнт кореляції є значущим, і лише у 5% випадків може виявитися рівним 0. Зауважимо, що, якщо зазначена нерівність стверджується для
, маємо констатувати, що коефіцієнт кореляції є значущим, і лише у 5% випадків може виявитися рівним 0. Зауважимо, що, якщо зазначена нерівність стверджується для 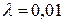 , то значущість коефіцієнта кореляції суттєво збільшується: лише 1% випадків він може виявитися рівним 0.
, то значущість коефіцієнта кореляції суттєво збільшується: лише 1% випадків він може виявитися рівним 0.
2 випадок. Коли число респондентів 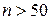 , необхідно вико-ристовувати
, необхідно вико-ристовувати 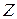 - критерій:
- критерій:
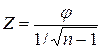 (12)
(12)
За таблицями критичних значень знаходимо величину Zкр для відповідного λ. Аналіз отриманих даних виконуємо аналогічно 1 випадку. Наведемо приклад визначення статистичної значущості коефіцієнта кореляції Пірсона для умов: 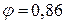 ;
; 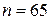 .
.
Тоді 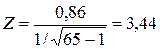 .
.
Для рівня значущості 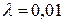 критичне значення
критичне значення 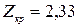 . Через те, що
. Через те, що 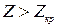 , маємо констатувати, що коефіцієнт кореляції
, маємо констатувати, що коефіцієнт кореляції 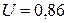 є значущим, і лише в 1% випадків може виявитися рівним 0.
є значущим, і лише в 1% випадків може виявитися рівним 0.
Перевірка статистичної значущості коефіцієнта кореляції Спірмена. Значущість коефіцієнта кореляції Спірмена визначається залежними від 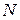 -числа пар рангів, що зіставляються у формулі (11).
-числа пар рангів, що зіставляються у формулі (11).
Якщо 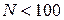 , значущість коефіцієнта кореляції можна визна-чити за таблицею, де наведено критичні значення величини
, значущість коефіцієнта кореляції можна визна-чити за таблицею, де наведено критичні значення величини 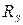 .
.
Наприклад, використовуючи дані таблиці, де 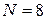 (менше 100), за таблицями додатку Г визначаємо, що для того, щоб
(менше 100), за таблицями додатку Г визначаємо, що для того, щоб 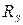 був значущим на рівні
був значущим на рівні 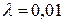 , він має бути рівним, або більшим за 0,833. Емпіричне (вирахуване) значення коефіцієнта кореляції Спірмена за формулою (11) дорівнює 0,89, тому робиться висновок, що є значущий зв’язок між мотивами навчання студентів-першокурсників агрономіч-ного та юридичного факультетів аграрного університету.
, він має бути рівним, або більшим за 0,833. Емпіричне (вирахуване) значення коефіцієнта кореляції Спірмена за формулою (11) дорівнює 0,89, тому робиться висновок, що є значущий зв’язок між мотивами навчання студентів-першокурсників агрономіч-ного та юридичного факультетів аграрного університету.
Якщо 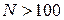 , то критичні значення знаходяться за таблицею t – розподілення Стьюдента. Емпіричні значення критерію Z вираховуються за формулою:
, то критичні значення знаходяться за таблицею t – розподілення Стьюдента. Емпіричні значення критерію Z вираховуються за формулою:
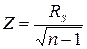 , (13)
, (13)
де 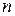 – число респондентів.
– число респондентів.
Дата добавления: 2015-11-06; просмотров: 911;
