Основні поняття математичної статистики
При аналізі багатьох педагогічних явищ важливу роль відіграють середні величини, які дозволяють глибше зрозуміти особливості об’єкта спостереження. У математичній статистиці є декілька видів середніх величин: середнє арифметичне, медіана, мода і т.ін. Крім того, існує декілька показників коливання (міри розсіювання): варіа-ційний розмах, середнє квадратичне відхилення, середнє абсолютне відхилення, дисперсія тощо.
Середнє арифметичне є абстрактною типовою характеристикою цієї сукупності. Воно згладжує, нівелює випадкові й невипадкові коливання, вплив індивідуальних особливостей та дозволяє подати однією величиною деяку загальну характеристику реальної сукупності одиниць. Середнє арифметичне вираховується як частина від поділу суми величин на їх число і вираховується за формулою:
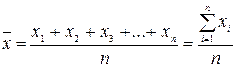 , (1)
, (1)
де 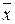 – середнє арифметичне;
– середнє арифметичне;
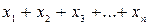 – результати окремих спостережень, значення ознаки;
– результати окремих спостережень, значення ознаки;
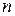 – кількість спостережень;
– кількість спостережень;
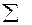 – сума результатів усіх спостережень.
– сума результатів усіх спостережень.
Приклад: вирахуємо середнє число годин, які щоденно витра-чаються студентами на самостійну роботу (у вибірці із 20 осіб) (табл. 8.1).
Таблиця 8.1
Витрата часу студентами групи А-2 на самостійну роботу (год.)
| i | ||||||||||||||||||||
| t | 2,2 | 3,2 | 1,9 | 3,0 | 2,8 | 4,0 | 1,9 | 2,3 | 2,9 | 3,3 | 2,0 | 3,7 | 1,7 | 2,4 | 3,3 | 1,8 | 1,7 | 3,4 | 3,2 | 1,9 |
Знаходимо загальну суму часу, який витрачають опитані на самостійну роботу:
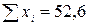 год.
год.
За формулою (1) знаходимо:
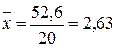
При обрахуванні середнього арифметичного для згрупованих даних формула (1) має вигляд:
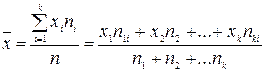 , (2),
, (2),
де 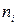 – частота для і-го значення ознаки.
– частота для і-го значення ознаки.
Процедура знаходження середнього за згрупованими даними виконується за схемою, яка наведена у табл.8.2.
Таблиця 8.2
| Інтервал | Середина інтервалу ( 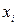 ) )
| Частота (відносна) 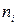
| Добуток
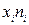
|
| Послідовно записуються усі інтервали | 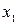
| 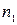
| 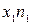
|
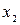
| 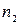
| 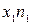
| |
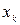
| 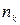
| 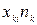
| |
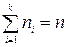
| 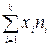
|
Приклад. Наведені дані щодо щоденної витрати часу на самостійну роботу групою студентів із 20 осіб згрупуємо й продемонструємо у табл. 8.3.
Таблиця 8.3
| Інтервал, год. | Середина інтервалу 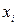
| Частота (відносна) 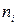
| Добуток
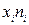
|
| 1 – 2 | 1,5 | 10,5 | |
| 2 – 3 | 2,5 | 12,5 | |
| 3 – 4 | 3,5 | ||
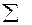
| 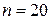
| 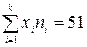
|
Звідси вираховуємо:
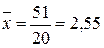 год.
год.
Медіаною називається значення досліджуваної ознаки, зліва і справа від якої знаходиться однакова кількість елементів вибірки за шкалою, побудованою за зростанням чи зменшенням чисел. Місце розташування медіани визначається за формулою:
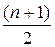 (3)
(3)
Якщо в ряду парне число членів ( 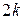 ), то медіана дорівнює середньому арифметичному з двох серединних значень ознаки; при непарному числі членів (
), то медіана дорівнює середньому арифметичному з двох серединних значень ознаки; при непарному числі членів ( 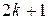 ) медіанним буде значення ознаки у (
) медіанним буде значення ознаки у ( 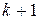 ) об’єкта.
) об’єкта.
Наприклад, у вибірці з 10 осіб респонденти проранжовані за пе-дагогічним стажем роботи на кафедрі (табл. 8.4).
Таблиця 8.4
Дані щодо педагогічного стажу викладачів кафедри
| Ранг викладача | ||||||||||
| Педагогічний стаж |
Знаходимо місце медіани: 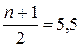 (серединні значення 5 і 6).
(серединні значення 5 і 6).
Звідси медіана дорівнює:
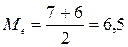
За результатами визначення медіани можна зробити висновок, що більше половини викладачів кафедри мають стаж 6,5 років.
Варто додати, що:
- медіана ділить впорядкований варіаційний ряд на дві рівні по чисельності групи;
- квартилі ділять ряд розподілу на 4 рівні частини;
- процентилі ділять множину на 100 частин з рівним числом спостережень у кожній;
- децилі ділять множину спостережень на 10 рівних частин;
Квантилі (квартилі, процентилі, децилі) легко вираховуються за розподілом накопичених частот.
Модоюу статистиці називають значення ознаки, яке найчастіше зустрічається і з яким найбільш вірогідно можна зустрітися в серії зареєстрованих спостережень. Іншими словами, – це типове значення ознаки, яке найчастіше зустрічається серед інших значень. Мода від-повідає класу з максимальною частотою. Цей клас називають модальним значенням.
У дискретному ряді мода ( 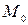 ) – це значення з найбільшою частотою. В інтервальному ряді (з рівними інтервалами) модальним є клас з найбільшим числом спостережень. При цьому значення моди знаходиться в його межах і вираховується за формулою:
) – це значення з найбільшою частотою. В інтервальному ряді (з рівними інтервалами) модальним є клас з найбільшим числом спостережень. При цьому значення моди знаходиться в його межах і вираховується за формулою:
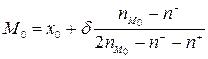 , (4)
, (4)
де 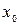 – нижня границя (межа) модального інтервалу;
– нижня границя (межа) модального інтервалу;
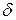 – величина інтервалу;
– величина інтервалу;
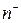 – частота інтервалу, який знаходиться попереду;
– частота інтервалу, який знаходиться попереду;
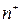 – частота інтервалу, наступного за модальним;
– частота інтервалу, наступного за модальним;
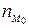 – частота модального класу.
– частота модального класу.
Приклад. На питання анкети: «Вкажіть ступінь володіння іно-земною мовою» відповіді 598 студентів першого курсу інженерних спеціальностей були такими:
- володію вільно – 31;
- володію достатньо для спілкування – 60;
- володію, але відчуваю труднощі при спілкуванні – 278;
- розумію важко – 195;
- не володію – 34.
Цілком очевидно, що типовим значенням у наведеному прикладі є «володію, але відчуваю труднощі при спілкуванні», яке і буде модальним. Таким чином, мода дорівнює 278.
До основних недоліків моди як виду середніх величин варто віднести:
- неможливість виконувати над модою алгебраїчні дії;
- залежність її величини від інтервалу групування;
- можливість існування в ряді розподілу декількох модальних значень ознаки.
Для характеристики рядів розподілу є недостатнім мати лише середні величини даної ознаки, бо два ряди, наприклад, можуть мати однакові середні арифметичні, але ступінь концентрації (чи «розки-дання») значень ознак навкруг середньої буде зовсім іншим. Характе-ристикою такого розкидання є показники розсіювання – дисперсія, середнє квадратичне відхилення, коефіцієнт варіації.
Дисперсієюназивають величину, рівну середньому значенню квад-рата відхилень окремих значень ознак від середньої арифметичної.
Дисперсія 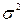 вираховується за формулою:
вираховується за формулою:
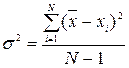 (5)
(5)
Послідовність вирахування дисперсії така:
- визначення відхилення від середнього значення;
- вирахування квадрата зазначеного відхилення;
- знаходження суми квадратів відхилення і середнього значення квадрата відхилень (табл. 5).
Приклад. За результатами виконання контрольної роботи сту-денти групи отримали такі оцінки: «відмінно» – 4 особи; «добре» – 8 осіб; «задовільно» – 5 осіб; «незадовільно» – 5 осіб. Для вирахування дисперсії оцінок студентів слід скласти таблицю (табл. 8.5).
Таблиця 8.5
| № п/п | Оцінка | Відхилення від середнього | Квадрат відхилення |
| -1,5 | 2,25 | ||
| 1,5 | 2,25 | ||
| -0,5 | 0,25 | ||
| 0,5 | 0,25 | ||
| -1,5 | 2,25 | ||
| 0,5 | 0,25 | ||
| 1,5 | 2,25 | ||
| -0,5 | 0,25 | ||
| 0,5 | 0,25 | ||
| 0,5 | 0,25 | ||
| -1,5 | 2,25 | ||
| 0,5 | 0,25 | ||
| -0,5 | 0,25 | ||
| 1,5 | 2,25 | ||
| 0,5 | 0,25 | ||
| -1,5 | 2,25 | ||
| 0,5 | 0,25 | ||
| -0,5 | 0,25 | ||
| 0,5 | 0,25 | ||
| 1,5 | 2,25 | ||
| -0,5 | 0,25 | ||
| -1,5 | 2,25 | ||
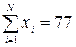
| 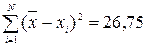
| ||
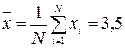
| 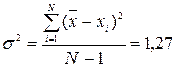
|
Цілком очевидно, що величина дисперсії не дозволяє спосте-рігачеві безпосередньо зробити певні узагальнення щодо розкиду досліджуваної змінної. Величиною, яка безпосередньо пов’язана зі змістовими характеристиками змінної, є середнє квадратичне відхилення. Середнє квадратичне відхилення підтверджує типовість і показовість середньої арифметичної та відображає міру коливання числових значень ознаки. Воно дорівнює кореню квадратному із дисперсії та визначається за формулою:
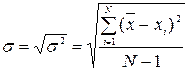 , (6)
, (6)
де 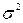 – дисперсія.
– дисперсія.
У попередньому прикладі щодо результатів виконання студентами контрольної роботи дисперсія дорівнює 1,27. Тоді середнє квадратичне відхилення буде:
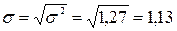 .
.
Отримані дані можна інтерпретувати таким чином: при середній оцінці 3,5 виконання контрольної роботи всі інші студенти групи мають оцінку, яка в середньому відхиляється від 3,5 на 1,13.
Середнє квадратичне відхилення є мірою абсолютного коливання ознаки і завжди виражається у тих самих одиницях вимірювання, що й ознака. Це не дозволяє зіставити між собою середні відхилення різних ознак, а також однієї й тієї ж ознаки у різних сукупностях. Щоб мати таку можливість, слід середні відхилення виразити у від-сотках до середнього арифметичного – у вигляді відносних величин. Відношення середнього квадратичного відхилення до середнього арифметичного називають коефіцієнтом варіації ( 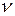 ):
):
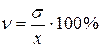 (7)
(7)
Природно, з двох порівнювальних рядів той має більший розкид, у якого коефіцієнт варіації більший.
Дата добавления: 2015-11-06; просмотров: 1399;
