Закон распределения вероятностей дискретной двумерной
Случайной величины
Законом распределения вероятностей двумерной дискретной случайной величины называют перечень возможных значений этой величины, т.е пар чисел (xi, yj) и их вероятностей p(xi, yj) 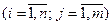 . Обычно закон распределения задают в виде таблицы с двойным входом (табл. 4.1).
. Обычно закон распределения задают в виде таблицы с двойным входом (табл. 4.1).
Первая строка таблицы содержит все возможные значения составляющей Х, а первый столбец - все возможные значения составляющей У. в клетке, стоящей на пересечении «столбца xi» и «строки yj», указана вероятность p(xi, yj) того, что двумерная случайная величина примет значение (xi, yj).
Так как события (Х=xi, У= yj) 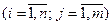 образуют полную группу, то сумма вероятностей, помещённых во всех клетках таблицы, равна единице.
образуют полную группу, то сумма вероятностей, помещённых во всех клетках таблицы, равна единице.
Таблица 4.1
| Значения у | Значения х | |||||
| х1 | х2 | … | xi | … | xn | |
| y1 | p(x1, y1) | p(x2, y1) | … | p(xi, y1) | … | p(xn, y1) |
| y2 | p(x1, y2) | p(x2, y2) | … | p(xi, y2) | … | p(xn, y2) |
| … | … | … | … | … | … | … |
| yj | p(x1, yi) | p(x2, yi) | … | p(xi, yj) | … | p(xn, yj) |
| … | … | … | ||||
| ym | p(x1, ym) | p(x2, ym) | … | p(xi, ym) | … | p(xn, ym) |
Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из её составляющих. Действительно, например, события (Х=х1; У=у1), (Х=х1; У=у2), …, (Х=х1; У=уm) несовместны, поэтому вероятность Р(x1) того, что Х примет значение х1, по теореме сложения такова: Р(x1)= p(x1, y1)+ p(x1, y2)+ … + p(x1, ym).
Таким образом, вероятность того, что Х примет значение х1, равна сумме вероятностей «столбца x1». В общем случае, для того, чтобы найти вероятность Р(Х= xi), надо просуммировать вероятности столбца xi. Аналогично, сложив вероятности «строки yj», получим вероятность Р(У=уj).
Пример 4.2. Найти законы распределения составляющих двумерной случайной величины, заданной законом распределения (табл. 4.2.1).
| Значе- ния y | Значения х | ||
| х1 | х2 | х3 | |
| у1 | 0,10 | 0,30 | 0,20 |
| у2 | 0,06 | 0,18 | 0,16 |
Решение. Сложив данные по столбцам, получим вероятности возможных значений Х, а именно: Р(х1)=0,16; Р(х2)=0,48; Р(х3)=0,36. Закон распределения составляющей Х двумерной случайной величины имеет вид Х х1 х2 х3 Проверка:
Р 0,16 0,48 0,36 0,16+0,48+0,36=1.
Сложив вероятности по строкам, получим вероятности возможных значений У, а именно: Р(у1)=0,60; Р(у2)=0,40. Закон распределения составляющей У будет иметь вид:
У у1 у2
Р 0,60 0,40 Проверка: 0,60+0,40= 1.
Дата добавления: 2015-11-06; просмотров: 883;
