Понятие о системе нескольких случайных величин

До сих пор мы рассматривали случайные величины, возможные значения которых определялись одним числом. Такие СВ называются одномерными. Например, число очков, которое может выпасть при бросании одного игрального кубика – дискретная одномерная СВ; расстояние от орудия до места падения снаряда – непрерывная СВ.

На практике часто приходится иметь дело с двумя, тремя и большим числом СВ или случайными величинами, возможные значения которых определяются двумя, тремя, … n числами. Такие величины называются, соответственно, двумерными, трёхмерными, …, n-мерными СВ. Например, 1) точка попадания снаряда характеризуется системой (Х, Y) двух случайных величин – абсциссой Х и ординатой Y. 2) успеваемость наугад взятого студента характеризуется системой n случайных величин (Х₁, Х₂, …, Х_n) - оценками, проставленными в его зачётной книжке.

Упорядоченный набор (Х₁,Х₂,…,Х_n) случайных величин , заданных на одном и том же пространстве элементарных событий (ПЭС) Ὠ, называется n-мерной случайной величиной или системой n случайных величин. Например, трехмерная случайная величина (Х, У, Z) определяет систему трёх случайных величин Х, У и Z.

Пример 4.1. Станок-автомат штампует стальные плитки. Если контролируемыми является длина Х и ширина У, то имеем двумерную случайную величину; если же контролируется и высота Z, то имеем трехмерную величину (Х, У, Z).

Двумерную случайную величину (Х, У) геометрически можно истолковать либо как случайную точку М(Х, У) на плоскости (т.е. как точку со случайными координатами), либо как случайный вектор 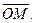Трёхмерную случайную величину, соответственно, геометрически можно интерпретировать либо как случайную точку М(Х, У, Z)в трёхмерном пространстве, либо как случайный вектор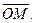

Целесообразно различать дискретные (составляющие этих величин дискретны) и непрерывные (составляющие этих величин непрерывны) многомерные случайные величины.