Стандартное нормальное распределение
Величину Х≈N(0, 1) с нулевым средним и единичным среднеквадратическим отклонением называют стандартной нормальной. Ее плотность вероятности и функция распределения задаются формулами:
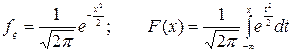 (3.11)
(3.11)
Определённый интеграл функции распределения не выражается через известные элементарные функции. Но данный интеграл в некоторых пределах может быть теми или иными приёмами вычислен с достаточной точностью точности. Определённый интеграл с переменным верхним пределом вида
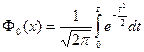 выражает площадь под кривой N(0, 1) в промежутке от 0 до z (рис. 3.3) и носит название функции Лапласа.
выражает площадь под кривой N(0, 1) в промежутке от 0 до z (рис. 3.3) и носит название функции Лапласа.
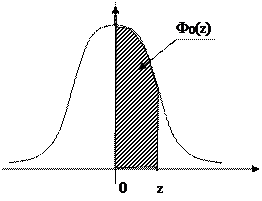 Ввиду важности этого по теории вероятности приводятся значения функции Лапласа для значений z от 0 до 5 через 0,01. Пользуясь таблицами нужно иметь в виду, что Ф0(0)=0; Ф0(-∞)=1/2; Ф0(+∞)=1/2;
Ввиду важности этого по теории вероятности приводятся значения функции Лапласа для значений z от 0 до 5 через 0,01. Пользуясь таблицами нужно иметь в виду, что Ф0(0)=0; Ф0(-∞)=1/2; Ф0(+∞)=1/2;
|
В силу симметрии функции f(х) относительно оси ординат достаточно задавать значения F(x) и Ф(х) только для положительных значений х. Легко видеть, что все три функции связаны простыми соотношениями, позволяющими по любой из них вычислить значения двух других
Пример 3.5. Затаривание мешков с сахаром производится без систематических ошибок. Случайные ошибки подчинены нормальному закону со среднеквадратическим отклонением σ = 200 г. Найти вероятность того, что затаривание будет проведено с ошибкой, не превосходящей по абсолютной величине 100 г.
Решение. В задаче рассматривается случайная величина – ошибка взвешивания, то есть разность между (ξ – а) – между случайным значением веса мешка сахара и его нормативным значением а – математическим ожиданием. Требуется найти:
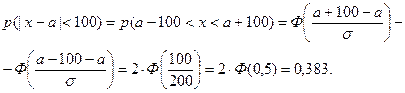
Дата добавления: 2015-11-06; просмотров: 889;
