Числовые характеристики системы двумерных случайных величин. Корреляционный момент, коэффициент корреляции.

Для описания системы двух случайных величин особую роль, кроме математического ожидания и дисперсии, играюткорреляционный момент и коэффициент корреляции.

Корреляционным моментом μ_ху случайных величин Х и У называют математическое ожидание произведения отклонения этих величин от их математических ожиданий, то есть

μ_ху = М{[Х-М(Х)]· {[У-М(У)]}

Для вычисления корреляционного момента дискретных величин используют формулу

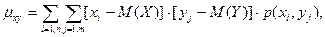
а для непрерывных величин – формулу

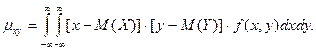
Корреляционный момент служит для характеристики связи между величинами Х и У. Как будет показано ниже, корреляционный момент равен нулю, если Х и У независимы; следовательно, если корреляционный момент не равен нулю, то Х и У - зависимые случайные величины.

Теорема 1. Корреляционный момент двух независимых случайных величин Х и У равен нулю.

Коэффициентом корреляции r_xy двухслучайных величин Х и У называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин

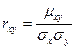
Так как размерность μ_ху равна произведению размерностей величин Х и У, ϭ_х имеет размерность величины Х, ϭ_у имеет размерность величины У, то r_xy – безразмерная величина. Таким образом, величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин. В этом состоит преимущество коэффициента корреляции перед корреляционным моментом.

Так как корреляционный момент равен нулю независимых случайных величин равен нулю (μ_ху =0), то и коэффициент корреляции независимых случайных величин также равен нулю (r_ху =0).

Теорема 2.Абсолютная величина корреляционного момента двухслучайных величин Х и У не превышает среднего геометрического их дисперсий:

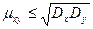
Теорема 3.Абсолютная величина коэффициент корреляции не превышает единицы