Свойства функции распределения двумерной случайной величины

1. Функция распределения F(x,y) ограничена, т.е. 0≤ F(х,у) ≤ 1.

2. Функция F(х,у) не убывает по каждому из своих аргументов при фиксированном другом, т.е.

F(х₂,у)≥ F(х₁,у) при х₂>х₁

F(х,у₂)≥ F(х,у₁) при у₂>у₁

3. Если хотя бы один из аргументов обращается в -∞, то функция распределения F(x,y) равна нулю, т. е.

F(х, -∞) = F(-∞, у) = F(-∞,-∞) = 0

4. Если оба аргумента обращаются в +∞, то функция распределения F(x,y) равна нулю, т. е. F(+∞,+∞) = 1.

5. Если один из аргументов обращается в +∞, то функция распределения системы случайных величин становится функцией распределения С.В., соответствующей другому элементу, т.е.

F(х, +∞) = F₁(x) = F_X(x), F(+∞, y) = F₂(y) = F_Y(y)

6. F(x,y) непрерывна слева по каждому из своих аргументов, т.е.

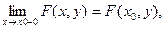
Плотность распределения вероятностей двумерной

Случайной величины

Непрерывную двумерную случайную величину можно также задавать, пользуясь плотностью распределения вероятностей. Будем полагать, что функция распределения F(x,y) всюду непрерывнаи имеет непрерывную частную производную второго порядка.

Плотностью совместного распределения вероятностей f(x,y) двумерной непрерывной случайной величины (Х, У)называют вторую смешанную частную производную от функции распределения:

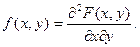
Зная плотностью совместного распределения f(x,y), можно найти функцию распределения F(x,y) по формуле