Реакции первого порядка

Кинетическое уравнение реакции первого порядка имеет вид:

v = - 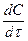= kC

гдe c - концентрация реагента.

Преобразовав уравнение, получим:

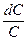- = kdt

и после интегрирования:

lnC = -kt +B

Обозначив начальную концентрацию как C_o (когда t=0) можно определить константу интегрирования B: B = lnC₀

Далее:

lnC = -kt + lnC₀ Þ (подставив lnC₀) lnC - lnC₀ = -kt Þ ln 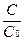= -kt

или (если найти антилогарифм): 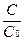=exp(-kt) and C= C₀×exp(-kt)

Диаграмма, где концентрация реагента представлена на оси ординат, время реакции - на оси абсцисс:

С

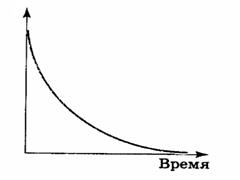
Представим, что нужно определить время, когда C= C₀/2 (концентрация исходного вещества упадет в 2 раза)

ln 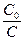= ln2 = -kt, t= =

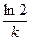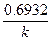
Эта зависимость показывает, что константа скорости реакции 1-го порядка обратно пропорциональна времени (периоду) полураспада.

Период полураспада (t_1/2) равен времени, в течение которого прореагирует половина первоначального количества вещества.

Также можно получить подобные уравнения для (t_1/2) для реакций более высокого порядка, но это более сложно.

Порядок реакций не равен их молекулярности если :

a) Один из реагентов присутствует в таком большом избытке, что его расход практически не будет изменять его концентрацию. Например, гидролиз эфира в разбавленном водном растворе:

CH₃COOC₂H₅ + H₂O = CH₃COOH + C₂H₅OH

Концентрация воды изменяется пренебрежимо мало, и скорость реакции будет зависеть только от изменения концентрации эфира. В результате скорость реакции будет описываться уравнением 1-го порядка, хотя это бимолекулярная реакция.

b) Если это сложная реакция. Обычно в этом случае уравнение химической реакции отражает только общий эффект всех взаимодействий

Например: 2N₂O₅ ® 4NO₂ + O₂

Молекулярность равна 2. Реакция имеет 2 стадии:

N₂O₅ ® N₂O₃ + O₂ (1)

N₂O₃ + N₂O₅® 4NO₂ (2)

1-я стадия - медленнее и определяет скорость суммарной реакции, поэтому v=kC_N2O5 и порядок реакции равен 1. Если одна из стадий проходит при низкой, по отношению к другим, скорости, то суммарная скорость реакции будет определяться скоростью этой стадии. Эта стадия называется - лимитирующая стадия реакции.

c) Для гетерогенных реакций, например:

2Zn + O₂ = 2ZnO. Молекулярность реакции равна 3, но кинетика реакции описывается уравнением реакции 1-го порядка: v= k×C_O2,

потому что Zn - это твердое вещество, у него нет концентрации, но O₂ - газ, ему соответствует определенная концентрация.

Сложные реакции

Кинетика сложных реакций, состоящих из 2-х и более простых реакций, взаимосвязанных друг с другом тем или иным способом, зависит от природы этой взаимосвязи и отношения скоростей простых реакций. Типичные формы взаимосвязи простых реакций, когда они являются параллельными, последовательными (консекутивные), сопряженными и обратимыми реакциями.

Теория кинетики сложных реакций основана на принципе, что когда несколько реакций происходят одновременно и каждая идет независимо и кинетика каждой реакции может быть описана кинетическим уравнением простой реакции.

Параллельные реакции - это реакции вида:

A ®B

¯

C

В таких реакциях начальное вещество (или вещества) могут реагировать параллельно в различных направлениях.

Например, 6KClO₃ ® 2KCl + 3O₂

¯

3KClO₄ + KCl

Последовательные реакции -реакции вида:

k₁ k₂

A ® B ® C

где B - промежуточный продукт в образовании C и k₁ и k₂ - константы скорости 2-х стадий реакции.

Сопряженные реакции - реакции типа:

A + B ® M

A + C ® N,

В которых одна, например 1-я, происходит только вместе со 2-й, т.е. индуцируется 2-й.

Обратимые реакции. Скорость обратимой реакции равна разности между скоростями прямой и обратной реакций.

Например:

v₁

H₂ + J₂ Û 2 HJ

v₂

v = v₁ - v₂ ,

если написать выражения для скоростей прямой и обратной реакций:

v₁ = k₁C_H2C_J2

v₂ = k₂C²_HCl

Если в системе первоначально присутствуют только реагенты (H₂ и J₂), скорость прямой реакции v₁ (Исходные вещества) будет уменьшаться с уменьшением концентраций этих компонентов.

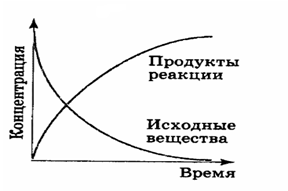
Кривая v₂ (Продукты реакции) начинается в начале координат (поскольку по условию первоначально C_HJ = 0) и возрастает по мере того, как реакция идет.

Положение равновесия будет достигнуто, когда абсолютное значение скоростей прямой и обратной реакций будет равным: v₁ = v₂ и результирующая скорость = 0.

Если переписать соотношение и затем преобразовать его:

k₁C_H2C_J2 = k₂C²_HCl

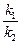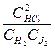= = K_c

где K_c - концентрационная константа равновесия реакции.

Если предыдущее уравнение применять к реакциям, проходящим в не очень разбавленных растворах, мы должны заменить концентрации веществ их активностями, и тогда заменить K_c на K_a.

Если уравнение применять к смеси идеальных газов мы должны заменить концентрации - парциальными давлениями газов, и соответственно K_c на K_p:

K_p=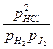

гдe p_HCl, p_H2, p_J2 - парциальные давления газов. Парциальное давление газа, находящегося в смеси других газов, равно давлению, которое этот газ производил, если бы он при данной температуре занимал весь объем, занимаемый смесью газов. В общем случае K_p ¹ K_c. Если применить уравнение для идеальных газов, можно найти зависимость между K_p и K_c.

p_i = 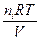= C_i RT

где n_i - количество молей газообразного компонента i, C_i - концентрация газа.

Tогда для вышеприведенной реакции:

K_p= 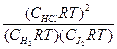= K_c (RT).

В общем случае: K_p = K_c (RT)^Dn ,

гдe Dn -разность между стехиометрическими коэффициентами газообразных продуктов реакции и реагентов (Для реакции (H₂ and J₂) Dn=0 and K_p = K_c)

Константа равновесия - важная характеристика реакции, по ее величине можно судить о степени протекания реакции (большое значение - реакция сдвинута в сторону продуктов реакции, низкое - в сторону исходных веществ). Константа не зависит от концентраций (давлений), зависит от температуры.

Если переписать уравнение реакции в общем виде:

aA + bB = cC + dD +eE

и вещества A, B, C and D - газы, а E - жидкость или твердое вещество, тогда:

Dn= c + d –a –b

Для условий: реакция проходит при постоянной температуре и постоянных парциальных давлениях для всех веществ, и законы идеальных газов применимы, существует связь между энергией Гиббса и константой химического равновесия K_p:

DG^o_{chem r.} = -RTlnK_p,

Таким образом, можно вычислить значение K_p