Й закон термодинамики

Введение. 1-й закон термодинамики определяет энергетические параметры процессов, и выводит соотношение связывающее изменение внутренней энергии системы с количествами поступившей теплоты и произведенной работы. 2-й закон терм. определяет направление процессов, т.е. определяет прежде всего какие из процессов в рассматриваемой системе могут протекать самопроизвольно, каково количество работы, которая может быть получена при этом, и каков предел возможного самопроизвольного течения процессов, т.е. каково состояние равновесия в данных условиях.

В отличие от первого закона, 2-й закон обладает более ограниченной областью применения. Он носит статистический характер и применим поэтому лишь к системам, состоящим из большого количества частиц, т.е. таким поведение которых может быть описано законами статистики.

Основные концепции.

Самопроизвольный процесс – это процесс, который протекает без приложения работы внешних сил над системой, в результате самопроизвольного процесса может быть получена полезная работа в количестве, пропорциональном произошедшим изменениям в системе.

Процессы, являющиеся результатом работы внешних сил над системой, также имеют место, в этом случае количество работы будет прямо пропорционально результирующим изменениям в системе.

Обратимый термодинамический процесс определяется как процесс, в котором система может возвратиться в свое первоначальное состояние при этом не наблюдается никаких изменений в самой системе и в окружающей среде. При необратимых термодинамических процессах систему можно вернуть после протекания процесса в ее первоначальное состояние, однако для этого необходимо затратить работу внешних сил.

2-й закон термодинамики:

Существует несколько формулировок, например:

- Тепло не может переходить самопроизвольно от менее нагретого тела к более нагретому;

- Невозможно создание вечного двигателя 2-го рода.

Для нас важна следующая формулировка:

- В изолированных системах только такие процессы могут проходить самопроизвольно в которых энтропия системы возрастает; процесс может проходить самопроизвольно до тех пор пока энтропия системы не достигнет своего максимального значения при данных условиях: DS³0

Таким образом, для каждой термодинамической системы в данных условиях существует общий критерий, который характеризует возможность, направление и предел протекания самопроизвольного процесса. Для изолированных систем – это термодинамический параметр называется энтропией.

Энтропия – это термодинамическая функция состояния, изменение которой для обратимого изотермического процесса равно приведенной теплоте процесса:

DS = 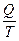или dS =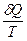

Данная формула может быть использована для расчета DS фазовых переходов.

Для необратимых процессов dS > .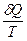

В общем случае математическое выражение 2-го закона термодинамики: dS ³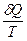

Энтропия является функцией состояния, следовательно, бесконечно малое изменение энтропии выражается полным дифференциалом dS, и изменение энтропии системы в данном процессе зависит только от первоначального и конечного состояний и не зависит от пути перехода.

DS = S₂ – S₁

Для химических реакций : DS_{х р.} = å(nS⁰)_прoд - å(nS⁰)_рeaг

гдe S⁰ - энтропия вещества в стандартных условиях.

Установление статистической природы 2-го закона термодинамики привело Больцмана (1896) к статистической интерпретации энтропии. Им было показано, что

S = k×lnP_th,

где k - константа Больцмана:

k = ,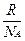

где R – универсальная газовая постоянная, N_A - число Авогадро = 6.0×10²³ мoль⁻¹,

P_th - термодинамическая вероятность данного состояния системы. Статистический характер энтропии проявляется в том, что данная вероятность нахождения системы в данном состоянии (как макросостояние) представляет собой результат вкладов огромного числа числа микросостояний, в котором находятся частицы этой системы. Энтропия может рассматриваться, как сумма составляющих, относящихся к различным формам движения частиц. По характеру движения рассматривают следующие составляющие S: энтропия поступательного движения молекул, энтропия вращательного движения молекул, энтропия вращательного движения атомов и атомных групп, содержащихся в молекуле,энтропия колебательного движения атомов и атомных групп, содержащихся в молекуле, энтропия движения электронов.

Постулат Планка ( 3-й закон термодинамики)

Математически постулат Планка может быть выражен выражением: 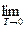S = 0.

При абсолютном нуле температуры энтропия идеальных кристаллических элементов или соединений в чистом состоянии равна нулю, во всех других состояниям – больше нуля.

Физическая интерпретация энтропии – энтропия может рассматриваться как мера беспорядка (или упорядоченности) в организации (структуре) частиц вещества. Поэтому энтропия имеет минимальное значение для идеальных кристаллических тел.

Характеристические функции и термодинамические потенциалы

Характеристической функцией называется функция состояния системы, посредством которой или ее производных могут быть выражены в явной форме термодинамические свойства системы. Наиболее широко в термодинамике используются следующие 5 характеристических функций:

- изобарно-изотермический потенциал (или свободная энергия Гиббса);

- изохорно-изотермический потенциал (св. энергия Гельмгольца);

- внутренняя энергия;

-энтальпия;

-энтропия.

Первые 4 объединяется общим названием термодинамические потенциалы. Этот термин также часто используется в более узком смысле обозначая им только первые 2 функции – энергию Гиббса и энергию Гельмгольца.

Критерии направления самопроизвольных процессов. Максимальная работа и максимальная полезная работа процесса

Из 2-го закона термодинамики dS ³ ,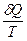

- для адиабатных процессов (dQ=0), для изолированных систем dS³0 критерий направленности самопроизвольного процесса

- для изотермических процессов (T - const): TdS³dQ,

Если подставить выражение для dQ в 1-й закон термодинамики:

dU=dQ - dA,

получим dU £TdS - dA и dA £ TdS – dU

В этих зависимостях знак равенства относится к равновесию и обратимым процессам, знак неравенства относится к необратимым процессам.

Последнее соотношение показывает, что работа, которую может совершить система, максимальна для обратимых процессов. Она называется максимальной работой и обозначается A_max

dA_max = TdS – dU

Для изотермических процессов (T - const) можно получить для какого-либо конечного процесса (конечного изменения):

A £ T(S₂ - S₁)-(U₂-U₁) и затем, преобразовав правую часть, и группируя:

A £ (U₁- TS₁) – (U₂ -TS₂)=- DF

Обозначив F= U- TS, как функцию, для которой можно написать:

dF= dU- TdS or DF= DU- TDS

Эта функция называется свободная энергия Гельмгольца, она играет важную роль в изучении равновесий изотермических процессов; обозначается F

Понятно, что dA_max =- DF

Как было показано раньше, изменение энтропии определяет направление пределы протекания самопроизвольных процессов в изолированных системах. Энергия Гельмгольца дает подобный критерий для систем при постоянном объеме и температуре: если DF£0 – процесс будет самопроизвольным при постоянным V и T.

Функцией, подобной энергии Гельмгольца, является свободная энергия Гиббса (или энергия Гиббса). Она дает критерий самопроизвольного протекания процесса в изолированной системе при постоянном давлении и температуре.

Эта функция обозначается символом G и определяется следующим выражением:

G= H - TS или : G= U- TS + PV а также: G= F + PV

Для любого процесса: DG = DA + D(PV),

Для изобарного процесса: DG= DF + PDV

Для изотермического процесса: dG= dH – TdS and DG= DH - TDS

Поскольку A_max =-DF (как показано ранее для обратимых процессов) и D G= DF + PDV тогда DG= DF + PDV = -A_max + PDV и -DG=A_max - PDV. Обозначим: -DG = A^’_max

получим: A^’_max = A_max-PDV

A^’_max - это максимальная полезная работа, которая равна максимальной работе минус работа, совершаемая системой, против внешнего давления.

В системе при постоянной температуре и объеме только такие процессы могут идти самопроизвольно, которые ведут к уменьшению F:D F £ 0, причем пределом их протекания, т.е. условием равновесия, является достижение некоторого минимального для данных условий, значения функции F, т.e. критерием равновесия является:

dG=0 and d²G>0

Аналогично, в системе при постоянной температуре и давлении только такие процессы могут идти самопроизвольно, которые ведут к уменьшению G:DG £ 0

Процесс достигает равновесия когда функция G достигает минимального значения для данных условий, т.e. критерием равновесия является:

dG=0 and d²G>0

Из соотношения DG= DH - TDS следует:

-что при низких температурах, когда T®0, если DH меньше нуля, то DG £ 0

-и при высоких температурах, T®¥, если DS>0, то DG £ 0 .

Поэтому экзотермические процессы являются самопроизвольными при низких температурах, но спонтанность некоторых процессов может зависеть от температуры.