Т е о р е м а 1 (правило произведения). Если множество содержит элементов, а множество содержит n элементов, то их декартово произведение содержит элементов, т.е.
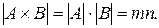 (4)
(4)
□ Пусть 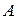 =
= 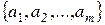 и
и 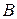 =
= 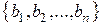 .Выпишем элементы множества
.Выпишем элементы множества 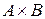 в виде прямоугольной таблицы:
в виде прямоугольной таблицы:
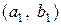 ,
, 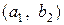 , …,
, …, 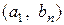 ,
,

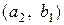 ,
, 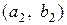 , …,
, …, 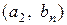 ,
,
…………………………………
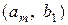 ,
, 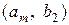 , …,
, …, 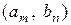 .
.
В этой таблице m строк и n столбцов и поэтому число ее элементов равно 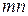 , что и доказывает равенство (4).
, что и доказывает равенство (4).
В комбинаторике это утверждение называют правилом произведения иформулируют следующим образом:
Правило произведения.Если элемент 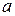 можно выбрать
можно выбрать 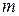 способами, а элемент
способами, а элемент 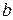 –
–  способами, то упорядоченную пару
способами, то упорядоченную пару 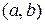 можно выбрать
можно выбрать 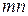 способами.
способами.
Теорема 1 обобщается на любое конечное число множителей в декартовом произведении.
Т е о р е м а 2 (обобщенное правило произведения).Если конечные множества 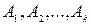 содержат соответственно
содержат соответственно 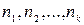 элементов, то множество
элементов, то множество 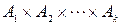 имеет
имеет 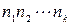 элементов, т.е.
элементов, т.е.
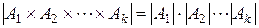 . (5)
. (5)
□ Применим индукцию по числу 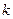 .
.
База индукции.При 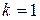 равенство (5) справедливо.
равенство (5) справедливо.
Шаг индукции.Предположим истинность равенства (5) для 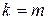 , т.е. что
, т.е. что
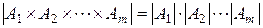 , (6)
, (6)
и рассмотрим 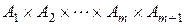 . Легко видеть, что
. Легко видеть, что
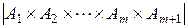 =
= 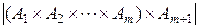 (7)
(7)
(это равенство вытекает из существования взаимно‑однозначного соответствия
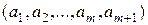

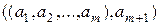
между множествами 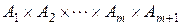 и
и 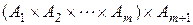 ). Используя теорему 1 и предположение индукции (6), отсюда получаем
). Используя теорему 1 и предположение индукции (6), отсюда получаем
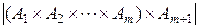 =
= 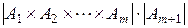 =
= 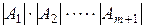 . (8)
. (8)
Из (7) и (8) следует теперь,
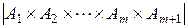 =
= 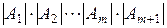 .
.
Таким образом, мы доказали, что равенство (5) справедливо при 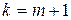 .
.
Вывод.На основании обычного принципа математической индукции равенства (5) истинно при любом натуральном 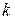 .
.
Дата добавления: 2015-11-04; просмотров: 745;
