Соединения без повторений

В этом разделе будут рассмотрены три вида соединений без повторений: размещения, перестановки и сочетания. Ради краткости добавку «без повторений» будем опускать.

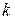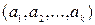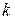1. Размещения.Размещения из n элементов по – это упорядоченные наборы из попарно различных элементов -множества 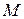. Таким образом, два размещения из элементов по 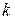различаются либо порядком, либо составом входящих в них элементов. Например, размещения из 3-множества по 2 исчерпываются следующими упорядоченными парами:

, , , , , .

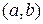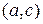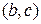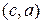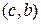Нас будет интересовать задача нахождения числа всех размещений из элементов по 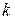. В качестве первого элемента 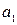можно выбрать любой из элементов множества 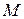. После того как выбран первый элемент, второй элемент 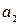можно выбрать лишь способами (можно взять любой элемент, исключая выбранный). После выбора первых двух элементов остаются лишь 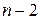возможности выбрать третий элемент и т. д. Последний 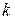-й элемент можно выбрать 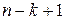способами – ведь до него уже выбраны элемент, а потому осталось лишь элементов. По правилу произведения получаем, что число всевозможных упорядоченных наборов 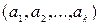равно произведению чисел , , , 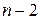…, , 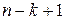т.е. справедлива следующая

Т е о р е м а 1.Число размещений из элементов по 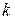находится по формуле

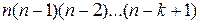= . (1)

Напомним, что произведение первых n натуральных чисел, т.е. 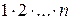, называют n-факториалом и обозначают 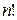. Произведение 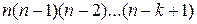можно записать в виде дроби 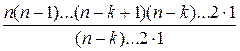= 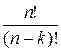и поэтому формулу (1) можно переписать следующим образом

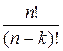= . (2)

В частности, при 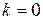из формулы (2) получаем

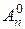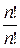= = 1.

Это означает, что существует единственный упорядоченный набор длины 0 – пустой кортеж, не имеющий ни одной компоненты.

Пример 1.Найти число пятизначных чисел в десятичной системе счисления, в записи которых цифры не повторяются.

□ Рассуждая по аналогии с тем, как это делалось при рассмотрении примера 1 (2-й способ) из § 2, приходим к выводу, что искомое число есть .

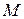2. Перестановки.Рассмотримтеперь различные линейные упорядочения данного -множества . Получаемые при этом упорядоченные наборы 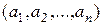отличаются друг от друга лишь порядком входящих в них элементов. Их называют перестановками (без повторений) из n элементов, а их число обозначают через 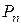. Например, если , то 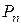= 6, так как из трех элементов 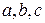можно составить шесть перестановок:

, , , , , .

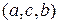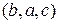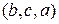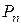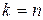Общая формула для получается из формулы (1), поскольку перестановка из элементов – это то же самое, что размещение без повторений из элементов по . Полагая в (1) получим = = = = 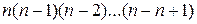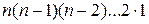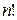. Итак, справедлива

Т е о р е м а 2.Число перестановок из элементов равно -факториал, т.е.

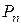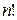= . (3)

Полагая в формуле (2) 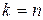, получаем

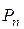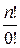= . (4)

Сравнивая (3) и (4), приходим к выводу, что 0! = 1. На первый взгляд это равенство кажется парадоксальным. Но для всех 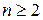справедливо равенство 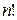= 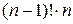. Если потребовать, чтобы это равенство было справедливо и при 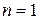, то получим 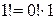. Отсюда вновь следует, что естественно положить0! = 1.

Пример 2.Сколькимиспособамиможно расположить на полке 7 различных учебников так, чтобы «Алгебра» и «Геометрия» не стояли рядом?

□ Условимся указанные учебники обозначать для краткости буквами А и Г соответственно. Число всевозможных способов расстановки учебников равно числу перестановок из семи элементов, т.е. 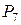. Но при этом сосчитаны и те, в которых встречаются рядом учебники А и Г, причем в двух позициях: АГ и ГА. Считая АГ и ГА за одну книгу, для каждого такого расположения получим 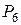расстановок, в которых учебники А и Г встречаются рядом. Искомое число расстановок учебников равно .

3. Сочетания.Одной из важнейших задач комбинаторики является подсчет числа k-подмножеств данного n-множества 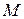. Такие неупорядоченные подмножества называются сочетаниями из элементов по 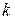, а их число обозначают через 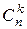(от французского слова combinaison – сочетание). Например, из элементов 4-множества 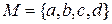можно составить следующие 2-множества: 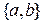, , , , 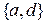, 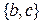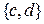. Число этих подмножеств равно 6. Следовательно, 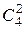= 6. Отметим, что = 1, так как каждое множество имеет лишь одно 0-множество, а именно, пустое множество 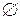. Далее понятно, что 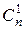= , поскольку в ‑множества 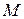содержится одноэлементных подмножеств. Ясно также, что .

Выведем формулу, выражающую 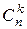через и 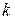. Для этого укажем способ получения всех размещений из элементов по 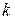. Выберем любое k-подмножество данного n-множества 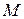. Это можно сделать 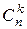способами. Каждое такое k-подмножество упорядочим всевозможными способами. Таких различных упорядочений столько, сколько можно составить перестановок из 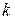элементов, т.е. 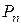= 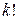. Понятно, что таким способом получатся все размещений из элементов по 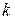. Значит, имеет место равенство = 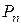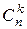. Отсюда вытекает справедливость следующего утверждения.

Т е о р е м а 3.Число сочетаний из n элементов по k вычисляется по формуле:

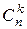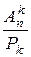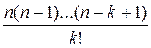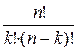= = = . (5)

Пример 3.Найти число всех диагоналей правильного n-угольника.

□ Любые две вершины n-угольника однозначно определяют отрезок, соединяющие эти вершины. Поэтому число всевозможных отрезков, соединяющих вершины n-угольника, равно числу сочетаний из по 2, т.е. 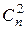. Но среди них находятся и сторон n-угольника, которые диагоналями не являются,

Таким образом, искомое число равно

.

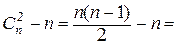
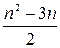Например, при 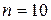получаем, что правильный 10-угольник имеет 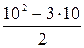= 35 диагоналей.