Свойства биномиальных коэффициентов.

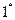. Биномиальные коэффициенты, равноудаленные от концов правой части равенства (1), равны.

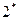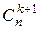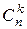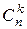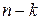. Для нахождения коэффициента , непосредственно следующего за коэффициентом , надо умножить на и поделить на .

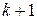Пример 1.Пользуясь свойствам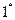и и 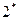, легко находим, что

.

Например, коэффициент при равен 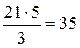. Найдя первую половину коэффициентов, вторую выписывают автоматически.

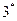. Зная коэффициенты разложения 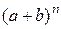можно найти коэффициенты разложения 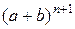, используя треугольник Паскаля.

Пример 2.Пользуясь табл. 2 и свойством 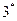, легко находим, что

.

Например, как это видно из табл. 2, коэффициент при равен сумме .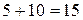

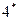. Сумма биномиальных коэффициентов равна .

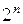Замечание 1. Это свойство можно получить из формулы (1). Действительно, положив в ней , получим 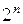= 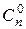+ + 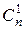…+ 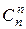. Тем самым другим методом доказана теорема 5 из § 2 о числе всех подмножеств ‑множества и , как следствие этого, свойство сочетаний.

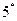. Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.

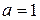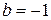□ В самом деле, положив в формуле (6) и , получим

0 = – + – + – …+ + … + .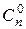

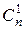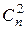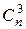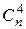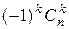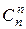Отсюда + + + … = + + +… .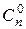

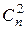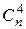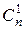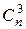Замечание 2.Формула (1) позволила нам найти новое свойство сочетаний.