Различные составы наборов длины n из элементов k‑множества называют также сочетаниями с повторениями из элементов по . Их число обозначают .

Итак, справедлива

Т е о р е м а 3.Число 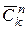всех сочетаниями с повторениями из 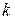элементов по вычисляется по формуле

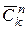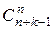= . (4)

Пример 3. Для множества всех букв, входящих в слово «Математика», число различных сочетаний с повторениями длины 10 равно = .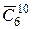

Вопросы для самоконтроля

1. Дать определение перестановки, сочетания и размещения без повторений. Вывести формулы для нахождения .

2. Сформулировать основные свойства чисел 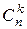и установить их связь с треугольником Паскаля и биномом Ньютона.

3. Решить задачи.

а) Сколько можно составить трехзначных чисел, если в каждом трехзначном числе любая цифра встречается только один раз?

б) Сколькими способами можно поставить на полке 10 различных книг, так чтобы выбранная книга стояла первой?

в) Сколькими способами можно сложить 6 различных книг в две сумки (порядок не имеет значения)?

4. Записать формулу исключений и включений для следующей задачи.

Часть жителей одного города умеют говорить только по-русски, часть только по-узбекски, а часть умеют говорить на обоих языках. По-узбекски говорят 85% жителей, по-русски – 75%. Сколько процентов жителей говорят на обоих языках?

5. Записать определение перестановок, сочетаний, и размещений с повторениями. Вывести соответствующие формулы.

6. Решить задачи:

а) Сколькими способами можно составить набор из 8 пирожных, если имеется 4 сорта?

б) Сколько нечетных трехзначных чисел можно составить из цифр 4, 5, 6?

в) Сколькими способами можно раскрасить трехполосный флаг, имея красный, белый и синий карандаши?

7. В чем суть принципа Дирихле? При решении каких комбинаторных задач он применяется?