В § 1 уже рассмотрен вопрос о числе размещений с повторениями. Для полноты картины, рассмотрим еще перестановки и сочетания с повторениями.
1. Перестановки с повторениями.Перестановкой с повторениями порядка n и состава 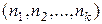 из элементов
из элементов 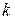 -множества
-множества 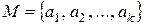 называется упорядоченная n‑ка, в которой элементы
называется упорядоченная n‑ка, в которой элементы 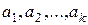 встречаются соответственно
встречаются соответственно 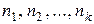 раз, причем
раз, причем 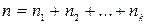 . Понятно, что две перестановки с повторениями одинакового порядка и состава могут отличаться друг от друга лишь порядком компонент. Например,
. Понятно, что две перестановки с повторениями одинакового порядка и состава могут отличаться друг от друга лишь порядком компонент. Например, 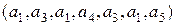 и
и 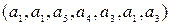 различные перестановки с повторениями порядка 7 и состава
различные перестановки с повторениями порядка 7 и состава 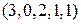 . Решим следующую комбинаторную задачу: найти число
. Решим следующую комбинаторную задачу: найти число 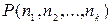 перестановок с повторениями порядка n, имеющих состав
перестановок с повторениями порядка n, имеющих состав 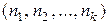 . Все такие перестановки можно получить следующим образом. Составим все перестановки без повторений из
. Все такие перестановки можно получить следующим образом. Составим все перестановки без повторений из  различных элементов, включающих элементы
различных элементов, включающих элементы 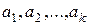 . Напомним, что их число
. Напомним, что их число 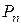 равно
равно 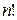 . Если
. Если 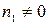 , то выберем произвольно
, то выберем произвольно 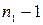 элементов, не входящих в множество
элементов, не входящих в множество 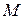 , и отождествим их с
, и отождествим их с 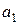 во всех перестановках. Легко понять, что таким образом получим перестановки с повторениями порядка
во всех перестановках. Легко понять, что таким образом получим перестановки с повторениями порядка  и состава
и состава 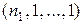 , где единица записана
, где единица записана 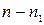 раз. Но различных среди них будет меньше во столько раз, сколько можно образовать перестановок без повторений из
раз. Но различных среди них будет меньше во столько раз, сколько можно образовать перестановок без повторений из 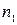 элементов, т.е. в
элементов, т.е. в 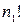 раз. Таким образом, получим
раз. Таким образом, получим 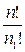 перестановок. Если
перестановок. Если 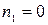 , то переходим к
, то переходим к 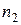 . Если
. Если 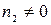 , то выберем произвольно
, то выберем произвольно 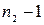 элементов, не входящих во множество
элементов, не входящих во множество 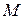 , и отождествим их с
, и отождествим их с 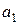 во всех перестановках. Легко понять, что таким образом получим
во всех перестановках. Легко понять, что таким образом получим 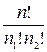 перестановок с повторениями порядка
перестановок с повторениями порядка  и состава
и состава 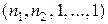 , где единица записана
, где единица записана 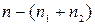 раз. Продолжая этот процесс, приходим к выводу о справедливости следующего утверждения:
раз. Продолжая этот процесс, приходим к выводу о справедливости следующего утверждения:
Т е о р е м а 1.Число 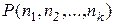 перестановок с повторениями порядка n, имеющих состав
перестановок с повторениями порядка n, имеющих состав 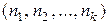 , вычисляется по формуле
, вычисляется по формуле
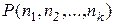 =
= 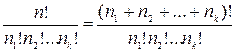 . (1)
. (1)
Пример 1. Буквы слова «Математика» можно переставлять 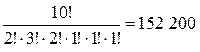 способами.
способами.
Из формулы (1) вытекает, что 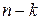 букв
букв 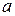 и
и 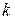 букв
букв 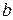 можно переставлять
можно переставлять 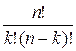 способами. Но это число равно
способами. Но это число равно 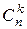 . Значит, число перестановок с повторениями состава
. Значит, число перестановок с повторениями состава 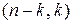 равно
равно 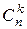 :
:
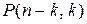 =
= 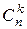 . (2)
. (2)
Формула (2) позволяет записать формулу бинома Ньютона в следующем виде:
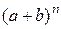 =
= 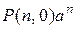 +
+ 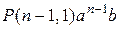 +…+
+…+ 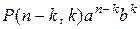 + … +
+ … + 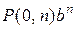 ,
,
или в краткой форме
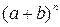 =
= 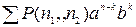 ,
,
где суммирование распространено на все наборы 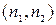 такие, что
такие, что 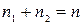 .
.
С помощью индукции по числу слагаемых нетрудно убедится в справедливости следующего утверждения:
Т е о р е м а 2.Длялюбых натуральных чисел  ,
, 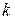 и любых действительных чисел
и любых действительных чисел 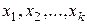 справедлива формула
справедлива формула
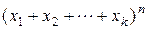 =
= 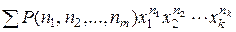 , (3)
, (3)
где суммирование распространено на все наборы 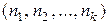 такие, что
такие, что 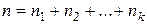 .
.
Пример 2. 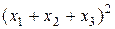 =
= 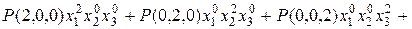
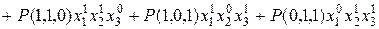 =
= 
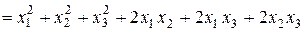 .
.
2. Сочетания с повторениями.Найдем теперь число различных составов, которые могут иметь наборы длины  , состоящие из элементов
, состоящие из элементов 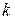 ‑множества
‑множества 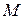 . Каждый такой состав является упорядоченным набором, состоящим из
. Каждый такой состав является упорядоченным набором, состоящим из 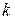 чисел
чисел 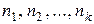 таких, что
таких, что 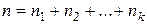 . Его можно записать в виде набора из нулей и единиц, заменив каждое число соответствующим числом единиц и поставив нуль после каждой группы единиц, кроме последней. Например, вместо набора
. Его можно записать в виде набора из нулей и единиц, заменив каждое число соответствующим числом единиц и поставив нуль после каждой группы единиц, кроме последней. Например, вместо набора 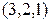 можно написать
можно написать 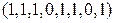 , а вместо набора
, а вместо набора 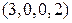 – набор
– набор 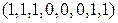 . Число единиц, входящих в полученные наборы, равно
. Число единиц, входящих в полученные наборы, равно 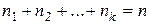 , а число нулей равно
, а число нулей равно 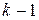 . Поэтому число различных наборов такого вида равно числу перестановок с повторениями из n единиц и
. Поэтому число различных наборов такого вида равно числу перестановок с повторениями из n единиц и 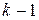 нулей, т.е..
нулей, т.е.. 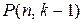 . Но ввиду формулы (2)
. Но ввиду формулы (2) 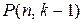 =
= 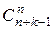 .
.
Таким образом, мы доказали, что число составов наборов длины  , компоненты которых принадлежат данному k‑множеству, равно
, компоненты которых принадлежат данному k‑множеству, равно 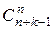 .
.
Дата добавления: 2015-11-04; просмотров: 1198;
