Свойства треугольника Паскаля.

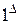. Числа, равноудаленные от концов треугольника Паскаля, равны.

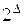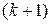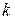. Для нахождения -го числа -й строки треугольника Паскаля надо умножить ‑ое на и поделить на .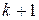

. Каждое число в треугольнике Паскаля равно сумме двух чисел, находящихся над ним.

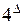. Сумма чисел n-ой строки треугольника Паскаля равна .

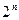Свойство позволяет легко заменить в таблице обозначения 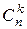конкретными числами, не пользуясь формулой числа сочетаний. Получаем следующую таблицу:

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

. . . . . . . . . .

Таблица 2.

Для получения этой таблицы надо на сторонах треугольника записать единицы, а внутренность угла при вершине заполнять, идя сверху вниз суммами стоящих рядом чисел предыдущей строки.

Например, число 10 в пятой строке табл. 2 получено сложением чисел 4 и 6 предыдущей строки.

Бином Ньютона

Приведем формулу для возведения суммы двух чисел в натуральную степень. Прежде всего, заметим, что числа стоящие с строках треугольника Паскаля, встречаются при возведении в степень двучлена :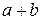

,

.

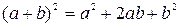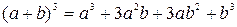Но коэффициенты 1, 2, 1 – это числа, стоящие во второй (напоминаем, что мы ведем счет с 0) строке таблицы 2, т.е. , а 1, 3, 3, 1 – числа, стоящие в третьей строке той же таблицы, т.е. .