Это замечание позволяет предположить, что справедливо следующее утверждение.

Т е о р е м а 5.Длялюбых чисел 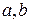и натурального числа справедлива формула

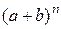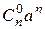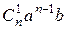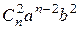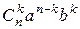= + + + … + + … + . (1)

□ Доказательство формулы (6) проведем индукцией по n, используя свойство 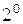сочетаний.

База индукции. При 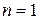имеем 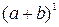= = 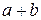+ 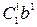и, следовательно, формула (1) справедлива.

Шаг индукции. Предположим, что формула (6) справедлива при 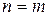, т.е.

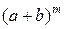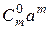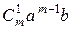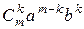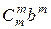= + + … + + … + . (2)

Чтобы доказать справедливость равенства (1) при 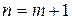, умножим обе части равенства (2) на :

= + + … + + … + .

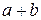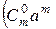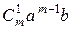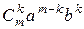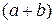Раскрывая скобки и приводя подобные в правой части последнего равенства, получаем

= + + … + + … + .

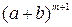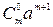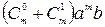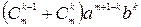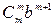Учитывая очевидные равенства = 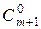, 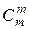= 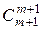и свойство 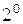сочетаний, имеем

= + + … + + … + .

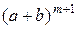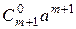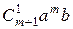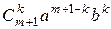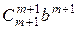Итак, формула (1) справедливо при 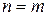+ 1.

Вывод. Формула (1) справедлива при любом натуральном .

Формулу (1) называют обычно формулой бинома Ньютона, хотя она была известна задолго до Ньютона уже упоминавшемуся Гиясэддину Каши, а также Паскалю и другим. Заслуга Ньютона состоит в том, что он нашел обобщение формулы (6) на случай нецелых показателей.

Формулу (1), учитывая, что 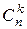= 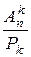, в развернутом виде можно переписатьв следующем виде:

= + + + …

…+ + … + + . ( )

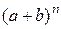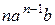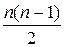
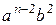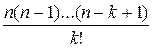
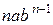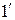С помощью формулы бинома Ньютона можно получить некоторые из доказанных ранее свойств сочетаний, а также вывести иные их свойства, и наоборот, свойства сочетаний позволяют упрощать вычисления коэффициентов в формуле (1). Числа 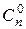, , 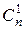…, называются биномиальными коэффициентами. Поскольку эти числа записаны в n‑ой строке треугольника Паскаля, то перефразируя его свойства получаем следующие