Кількісні показники надійності невідновлюваних ТО
За показники безвідмовності для такого класу ТО використовують: ймовірність безвідмовної роботи, частоту відмов, інтенсивність відмов, середнє напрацювання до відмови.
Серед показників надійності невідновлювальних систем основними є:
1) ймовірність безвідмовної роботи P(t);
2) ймовірність відмови Q(t);
3) середнє напрацювання на відмову T;
4) середній наробіток до відмови T0;
5) інтенсивність відмов l(t);
6) гамма-відсотковий наробіток tg ;
7) середній термін служби Tсл.
Ймовірність безвідмовної роботи – ймовірність того, що в заданому інтервалі часу t в ТО, або в його елементі не виникне відмова. Цей показник зв’язаний з функцією розподілу часу безвідмовної роботи наступним співвідношенням:
P(t) =1- Q(t), (5.1)
Очевидно, що 0< P(t) <1, P(0)=1, P(∞)=0.
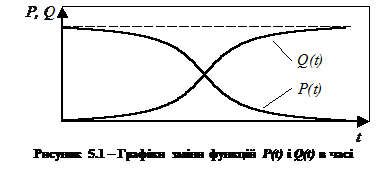
Слід відмітити, що P(t) є монотонно спадаючою функцією, а Q(t) – монотонно зростаючою функцією (рис. 5.1).
Для визначення величини P(t) використовується наступна статистична оцінка
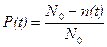, (5.2)
де N0 – число ТО, поставлених на випробування, або на експлуатацію; n(t) – число ТО, які відмовили на протязі часу t.
Частота відмов – це щільність розподілу часу безвідмовної роботи, або похідна від ймовірності безвідмовної роботи. Тому
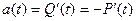. (5.3)
Для визначення величини a(t) використовується наступна статистична оцінка:
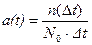, (5.4)
де n(Dt) – число ТО, які відмовили в інтервалі часу (t-Dt/2; t+Dt/2).
Покажемо справедливість вказаної оцінки. Число ТО, які відмовили на протязі часу Dt, дорівнює
,
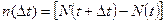де N(t) i N(t+Dt)– число ТО, які безвідмовно пропрацювали на протязі часу t i t +Dt відповідно.
При достатньо великому числі ТО, поставлених на випробування або експлуатацію, можна записати
;
.
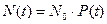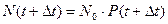Тоді
.
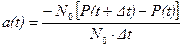При Dt ®0 отримаємо
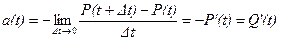. (5.5)
Між частотою відмов, ймовірністю безвідмовної роботи і ймовірністю появи відмови існують наступні залежності
, 
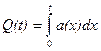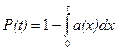. (5.6)
Наявність простої залежності між величиною a(t) і величинами Q(t) і P(t) є перевагою характеристики частоти відмов.
Інтенсивність відмов є умовною щільністю розподілу часу безвідмовної роботи для моменту часу t при умові, що до моменту часу t відмови ТО не було. Таким чином,
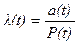. (5.7)
Так як P(t)<1, то, очевидно, завжди виконується співвідношення l(t)> a(t).
Для визначення величини l(t) використовується наступна статистична оцінка
,
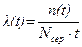де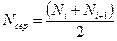 
– середнє число справно працюючих ТО в інтервалі часу Dt.
Покажемо справедливість вказаної оцінки. Враховуючи, що Nсер=N0-n(t), отримаємо:
.
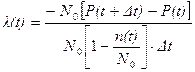При достатньо великому N0 можемо записати
:
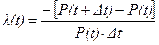При Dt®0 отримаємо
.
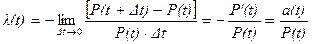Відмітимо важливу особливість, яка випливає з формули (5.7) для високонадійних ТО. ЯкщоP(t)>0,99, то a(t)» l(t). Допустима помилка складає не більше 1%, що, як правило, не перевищує помилок статистичного визначення величин a(t) і l(t).
Інтегруючи вираз (5.7), маємо:
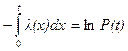, або 
.
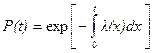Якщо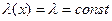 
, тоді
, 
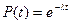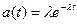. (5.8)
Порівняння формул (2.4) і (2.8) показує, що вказана заміна величин a(t) і l(t) базується на розкладі функції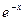 
в степеневий ряд.
Досвід експлуатації складних ТО показує, що інтенсивність відмов l(t) на протязі часу t змінюється так, як показано на рис. 5.2.
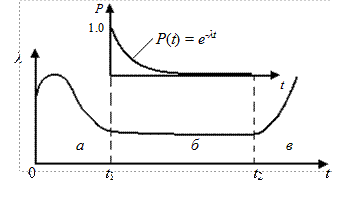
Як видно, функцію l(t) можна розділити на три ділянки. На першій ділянці а (0−t1) інтенсивність відмов висока і зменшується на протязі часу. На цій ділянці виявляються грубі дефекти виробництва, і сама ділянка носить назву ділянка припрацювання. Для складних ТО (систем управління об’єктами нафтогазового комплексу) тривалість цієї ділянки складає десятки, іноді сотні годин.
Друга ділянка б (t1− t2) – ділянка експлуатації, характерна тим, що інтенсивність відмов має постійне значення. Тривалість ділянки складає тисячі і десятки тисяч годин.
На третій ділянці в (t2−∞) через посилення процесів старіння елементів ТО інтенсивність відмов починає зростати.
Час t2 може служити часом, при досягненні якого ТО повинен зніматися з експлуатації.
Дата добавления: 2015-10-26; просмотров: 1458;