Експоненціальний (показовий) закон розподілу

Експоненціальним законом розподілу підпорядковується:

- Напрацювання на відмову ремонтованих і неремонтованих виробів при розгляді раптових відмов;

- Час безвідмовної роботи складних систем, що пройшли період припрацювання і складаються з елементів з різною інтенсивністю відмов.

При експоненціальному законі розподілу часу виникнення відмов мають місце такі залежності між основними кількісними характеристиками надійності:

1. Щільність ймовірності часу між відмовами:

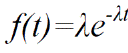(1)

де λ - інтенсивність відмов (параметр розподілу);

t - час безвідмовної роботи (випадкова величина).

2. Імовірність безвідмовної роботи:

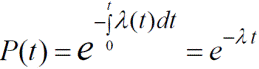(2)

3. Імовірність відмови, що представляє собою інтегральну функцію розподілу:

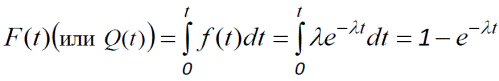(3)

4. Гамма-процентне напрацювання на відмову (до відмови):

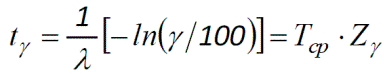(4)

де g - ймовірність безвідмовної роботи у відсотках,

Z_g - квантиль експоненціального закону розподілу.

5. Інтенсивність відмов:

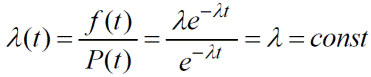(5)

6. Середній час безвідмовної роботи:

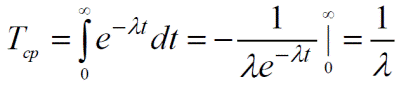(6)

Математичне сподівання наробітку до відмови не може досить повно охарактеризувати цю випадкову величину. Для більш повної характеристики надійності виробничих систем необхідно знати, принаймні, ще й її дисперсію:

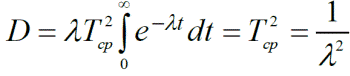(7)

Середнє квадратичне відхилення при цьому

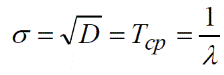(8)

Таким чином, при експоненціальному законі розподілу середнє квадратичне відхилення часу виникнення відмов рівне середньому часу безвідмовної роботи.

На практиці це властивість часто використовують для перевірки істинності гіпотези про існування експоненціального закону розподілу.

Якщо T_ср істотно відрізняється від s, це означає, що

експоненціальний закон для даної технічної системи несправедливий.

Графічне зображення основних кількісних характеристик надійності:

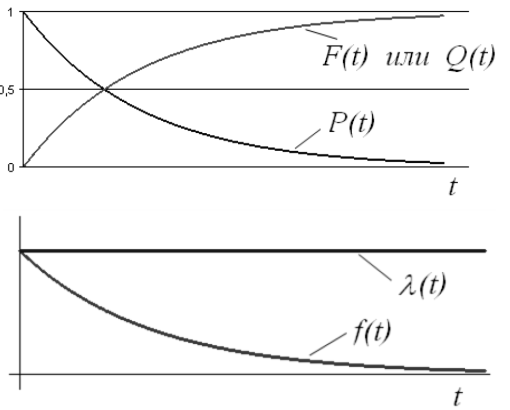
Нормальний закон розподілу (закон Гаусса)

Нормальному закону розподілу підпорядковуються:

- Час безвідмовної роботи виробничих систем, втрата працездатності яких пов'язана в основному з поступовими відмовами, при цьому частка раптових відмов вельми мала;

- Випадкові величини масових явищ, на які впливає велика кількість різних за величиною факторів (наприклад, знос і втома деталей, технологічні похибки, точність розмірів, одержуваних при обробці, і т. д.).

Нормальному закону розподілу підкоряються тільки неперервні випадкові величини. Тому нормальний розподіл може бути заданий:

- Або у вигляді щільності розподілу (диференціальної функції)

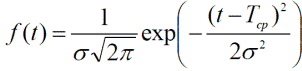(9)

- Або у вигляді інтегральної функції розподілу

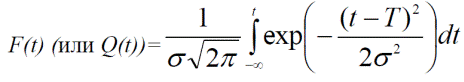(10)

де σ - середнє квадратичне відхилення;

t - час безвідмовної роботи (незалежна змінна);

T_ср - середній час (математичне очікування) безвідмовної роботи.

З формул видно, що нормальний розподіл є двопараметричний і визначається параметрами σ і T_ср.

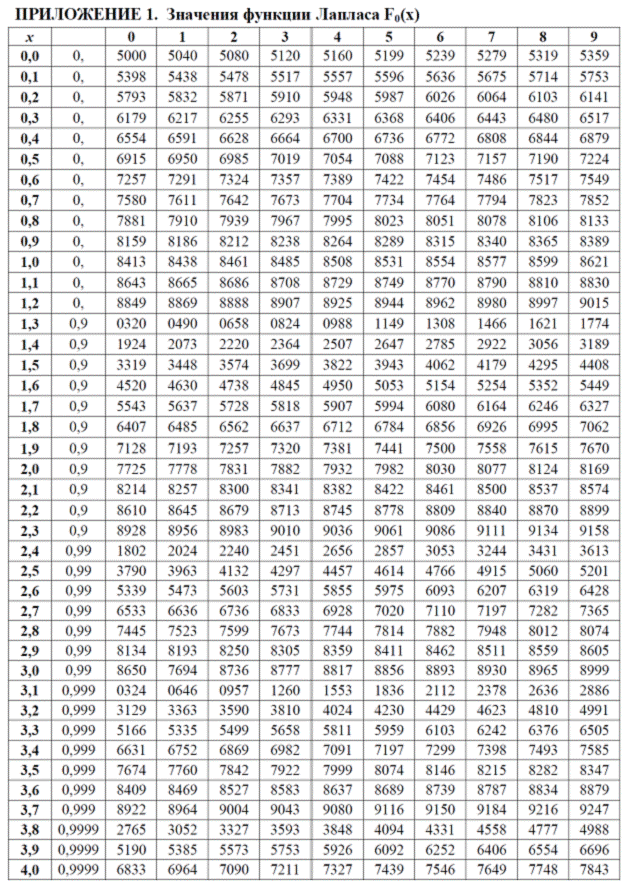
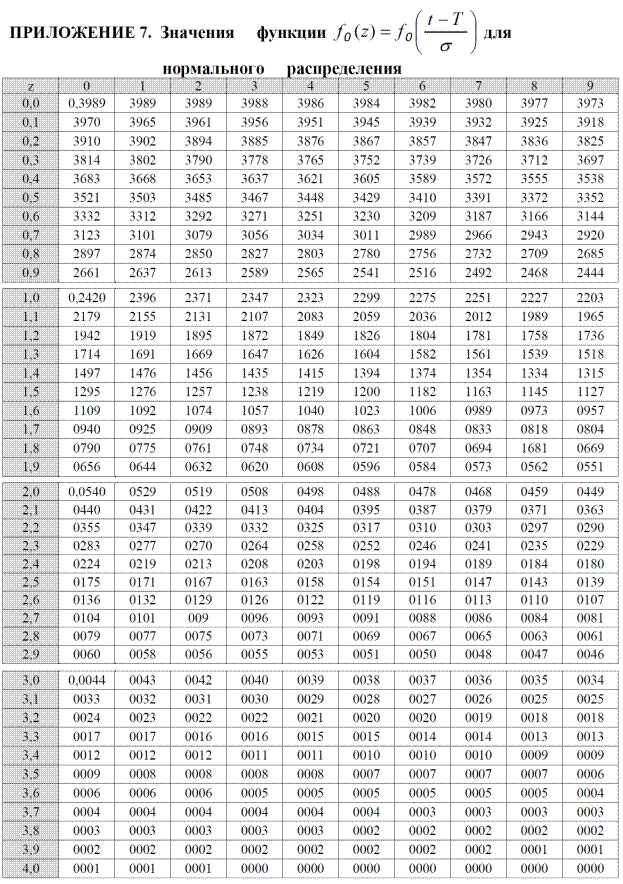
При T_ср=0 і s=1 виходить центрований і нормований розподіл, диференціальна f₀(t) і інтегральна F₀(t) функції якого табульовані і мають вигляд:

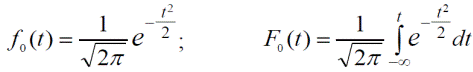(11)

Дотримуються наступні рівності:

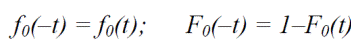(12)

Показники надійності при нормальному законі розподілу

визначаються за наступними формулами:

1. Імовірність відмови

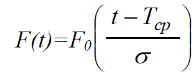(13)

2. Імовірність безвідмовної роботи

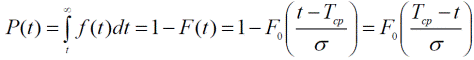(14)

3. Інтенсивність відмов,

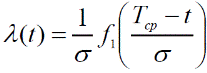(15)

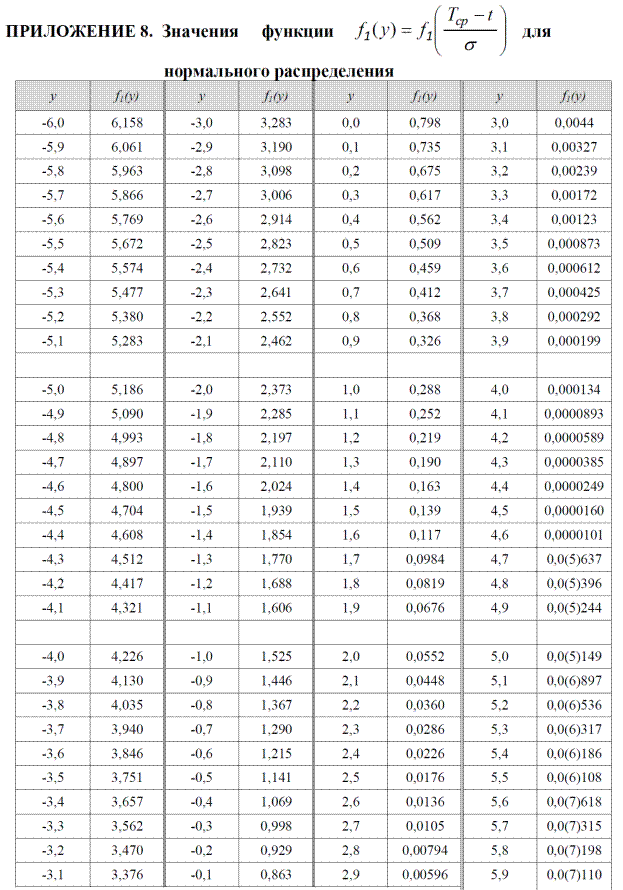
де f₁(t)=f₀(t)/F₀(t) - табульована функція.

4. Щільність розподілу (частота відмов)

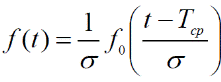(16)

5. Гамма-процентна напрацювання до відмови (на відмову)

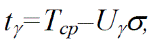(17)

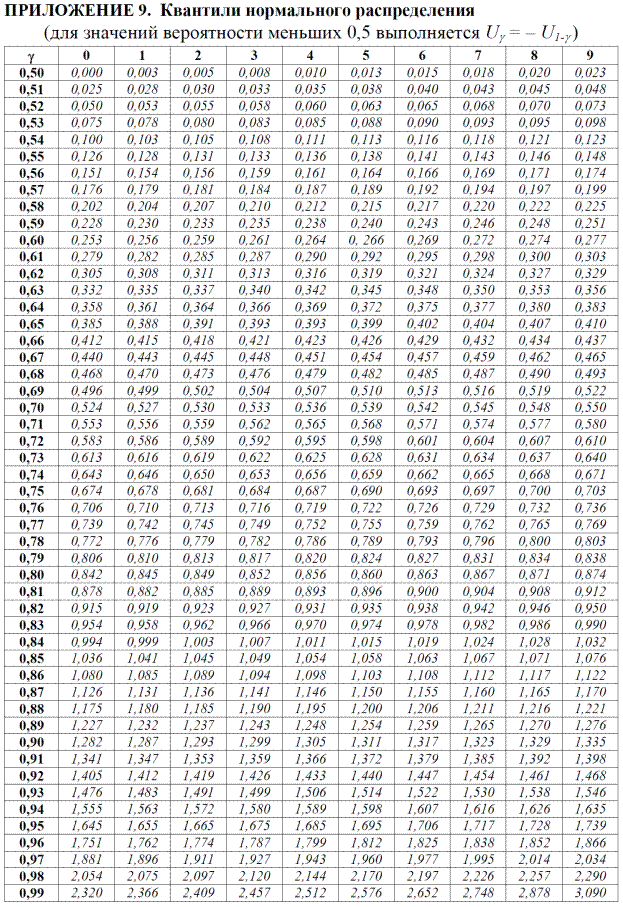
де U_g - квантиль нормального розподілу, тобто аргумент функції Лапласа, при якому F₀=g.

Графічне зображення основних характеристик надійності:

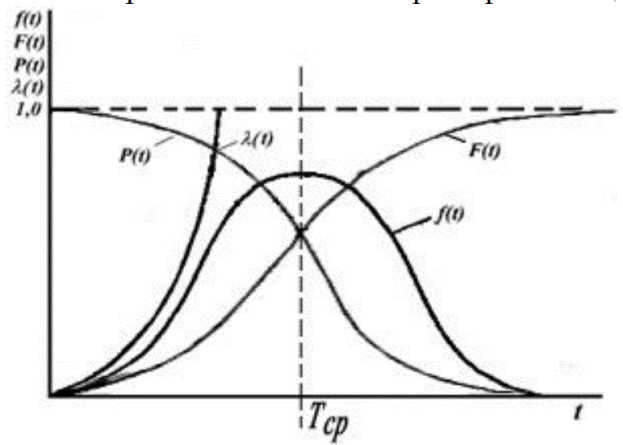
З графіків видно, що:

- Інтенсивність відмов має тенденцію до різкого зростання з плином часу, тобто потік відмов не є стаціонарним і має місце старіння елементів системи (поступові відмови);

- В області малих значень t старіння елементів чинить на надійність несуттєвий вплив, і тому ймовірність безвідмовної роботи з часом зменшується незначно;

- Диференціальна крива являє собою дзвоноподібну фігуру (криву Гауса), симетричну відносно прямої, що проходить через точку t=T_ср, звану центром розподілу.

Час безвідмовної роботи, що відповідає нормальному закону розподілу, має такі властивості:

- однакові позитивні і негативні відхилення від середньої арифметичної T_ср рівноможливі;

- менші відхилення більш вірогідні, ніж великі;

- вельми великі відхилення від T_ср малоймовірні;

- ймовірність того, що випадкова величина прийме значення, що знаходиться в межах від t₁ до t₂, може бути визначена за формулою

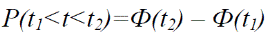(18)

де 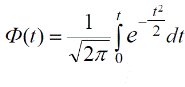- нормована функція Лапласа.