Закони розподілу відмов
В теорії надійності розглядають більше десяти законів розподілу відмов. Найбільше використання знайшли закони розподілу, наведені в таблиці 5.1.
В процесі експлуатації досить часто виникають відмови під впливом декількох факторів, що діють одночасно. Наприклад, обрив бурової колони, ослабленої корозією бурильних труб і їх зносом, при різкій зміні (збільшенні) осьового навантаження на долото. В таких випадках можна скористатися суперпозицією декількох законів розподілу (для наведеного прикладу можна поєднати експоненціальний та нормальний розподіл).
Таблиця 5.1 – Вирази для оцінки ймовірності безвідмовної роботи
| Закон розподілу відмов ТО | Вираз для ймовірності безвідмовної роботи | Графік розподілу |
| Показниковий (експоненціальний) | 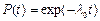 , , 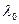 - інтенсивність відмов - інтенсивність відмов
| 
|
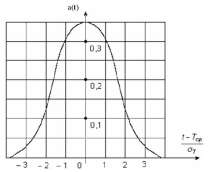
| Нормальний | 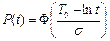
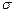 , , 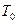 – параметри розподілу – параметри розподілу
| 
|
| Гамма (при цілому К) | 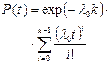
| 
|
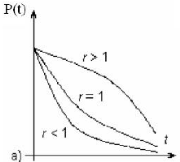
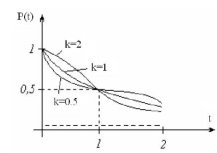
| Вейбулла | 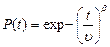 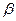 , , 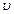 – параметри розподілу, при-чому – параметри розподілу, при-чому 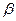 і і 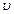 > 0 > 0
| 
|
| Релея | 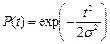
| 
|
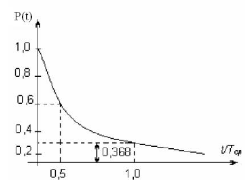
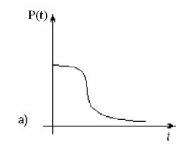
Інтенсивність відмов при експлуатації – постійна величина, яка не залежить від часу (рис. 5.2), тобто
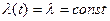 .
.
У відповідності з цим для інтервалу нормальної експлуатації
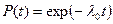 .
.
Експоненціальний закон розподілу – один із основних в теорії надійності.
З достатнім рівнем наближеності для деяких ТО чи їх елементів (в інтервалі ймовірності безвідмовної роботи 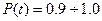 ) можна прийняти лінійну залежність ймовірності безвідмовної роботи від часу.
) можна прийняти лінійну залежність ймовірності безвідмовної роботи від часу.
Середнє напрацювання на відмову (середній час безвідмовної роботи) є математичним очікуванням напрацювання до першої відмови. Таким чином,
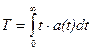 . (5.9)
. (5.9)
Цей вираз шляхом інтегрування по частинах може бути перетворено наступним чином:
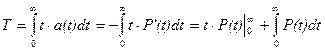 .
.
Враховуючи, що 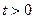 ,
, 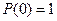 і
і 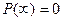 , в кінцевому виді отримаємо
, в кінцевому виді отримаємо
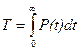 . (5.10)
. (5.10)
Для експоненціального закону розподілу часу безвідмовної роботи маємо
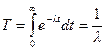 .
.
Для визначення середнього напрацювання до відмови використаємо наступну статистичну оцінку
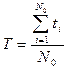 ,
,
де ti – час безвідмовної роботи і-го ТО.
Середнє напрацювання до відмови – математичне очікування напрацювання ТО, його елемента до відмови. Як математичне очікування неперервної випадкової величини, середнє напрацювання до відмови виражається через ймовірність безвідмовної роботи відомою залежністю:
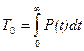 . (5.11)
. (5.11)
Для експоненціального закону розподілу
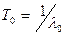 ,
,
тобто середнє напрацювання до відмови чисельно рівне величині, оберненій інтенсивності відмов.
Статистично середнє напрацювання до відмови визначається відношенням суми напрацювання експлуатованих до відмови tі ТО до кількості ТО чи їх елементів N, за якими ведеться спостереження, якщо всі вони відмовили за час спостереження:
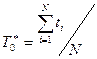 . (5.12)
. (5.12)
Для режимів зберігання і транспортування можуть використовуватись аналогічно визначені показники безвідмовності, наприклад, ймовірність виникнення відмови за час зберігання (транспортування).
За показники довговічності використовуються середні ресурс та строк служби.
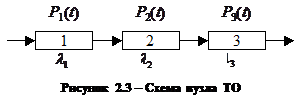 |
Середній ресурс – математичне очікування ресурсу, тобто напрацювання елементів ТО від початку експлуатації до настання граничного стану. Під граничним станом розуміють такий стан ТО та його елементів, при якому їх подальша експлуатація повинна бути припинена. Причинами цього можуть бути порушення вимог безпеки, вихід заданих параметрів за допустимі межі, які не можуть бути усуненими.
При наявності даних про ресурси 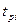 елементів ТО
елементів ТО 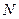 статистично оцінка середнього ресурсу обчислюється за формулою:
статистично оцінка середнього ресурсу обчислюється за формулою:
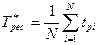 (5.13)
(5.13)
і визначається в годинах, кілометрах і т.п.
На практиці часто користуються гамма-процентним ресурсом 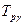 .
.
Гамма-відсотковий ресурс – напрацювання, на протязі якого ТО не досягне граничного стану з певною ймовірністю 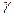 , вираженою у відсотках.
, вираженою у відсотках.
Його знаходять із рівняння
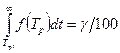 , (5.14)
, (5.14)
де 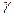 – заданий відсоток елементів, кожен з яких досягне установленого ресурсу
– заданий відсоток елементів, кожен з яких досягне установленого ресурсу 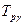 .
.
Наприклад, якщо був встановлений 80%-й ресурс 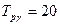 тис. год., це означає, що він повинен бути реалізований в експлуатації з ймовірністю 0.8, або 80% елементів ТО повинні відпрацювати 20 тис. год., а 20% – можуть вийти з ладу раніше.
тис. год., це означає, що він повинен бути реалізований в експлуатації з ймовірністю 0.8, або 80% елементів ТО повинні відпрацювати 20 тис. год., а 20% – можуть вийти з ладу раніше.
Між середнім і гамма-процентним ресурсом існує зв’язок, який визначається видом закону розподілу та його параметрами. Гамма-процентний ресурс пов’язаний із середнім наступним чином:
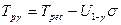 ,
,
де 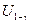 – квантиль закону розподілу ресурсу, під розуміють корінь рівняння
– квантиль закону розподілу ресурсу, під розуміють корінь рівняння 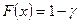 ;
; 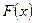 – функція розподілу ресурсу, значення якої табульовані.
– функція розподілу ресурсу, значення якої табульовані.
Наприклад, при 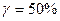 добуток
добуток 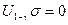 , так як
, так як 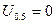 . В цьому випадку
. В цьому випадку 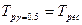 , тобто середній ресурс дорівнює гамма-процентному при
, тобто середній ресурс дорівнює гамма-процентному при 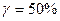 .
.
На практиці використовується назначений ресурс – сумарне напрацювання ТО, при досягненні якого використання за призначенням повинно бути припинене.
Середній термін служби – математичне очікування терміну служби, календарної тривалості експлуатації ТО чи його елемента від його початку до настання граничного стану. При наявності даних про термін служби 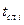 ТО і його елементів числом
ТО і його елементів числом 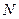 статистично оцінка середнього терміну служби обчислюється як
статистично оцінка середнього терміну служби обчислюється як
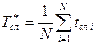 (5.15)
(5.15)
і визначається в добах, місяцях і т.п.
Основним показником зберігаємості є середній термін зберігаємості – математичне очікування терміну зберігаємості. Для оцінки впливу умов зберігання цей показник визначається як
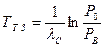 , (5.16)
, (5.16)
де 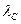 – інтенсивність відмов при зберіганні;
– інтенсивність відмов при зберіганні; 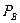 – значення ймовірності безвідмовної роботи ТО, його деталей, елементів до моменту використання;
– значення ймовірності безвідмовної роботи ТО, його деталей, елементів до моменту використання; 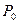 – значення ймовірності безвідмовної роботи ТО, його елементів в момент поступлення на технологічний процес чи об’єкт.
– значення ймовірності безвідмовної роботи ТО, його елементів в момент поступлення на технологічний процес чи об’єкт.
Лекція 6
Дата добавления: 2015-10-26; просмотров: 2983;
