Методика визначення закону розподілу показників надійності

План.

3. Етапи опрацювання експериментальних даних.

Література до лекції №7

6. Експлуатація та обслуговування машин: Конспект лекцій /Укладач В.Ф. Герман. – Суми: Вид-во СумДУ, 2009. - 98 с.

7. Тарасенко В.П., Маламан А.Ю. Надійність комп’ютерних систем. – Київ: Корнійчук, 2007. – 255с.

8. Иыуду К.А Надежность, контроль и диагностика вычислительных машин и систем. М: Высшая школа, 1989-216с.

9. Расулова С.С Надежность вычислительных машин и систем. Учебное пособие, ТашГТУ, 1995-60 с.

10. Локазюк В. М. Контроль і діагностування обчислювальних пристроїв та систем: Навч. посібник для вузів. – Хмельницький: ТУП, 1996. – 175 с.

11. Надежность автоматизированных систем управления / Аповмян И. О., Вайрадян А. С., Руднев Ю. П. и др. Под ред. Я. А. Хетагурова. – М.: Высшая школа, 1979. – 288 с.

Опрацювання експериментальних даних і розрахунок показників надійності виконуються в такій послідовності.

Поставимо перед собою завдання вивчити випадкову величину Т, закон розподілу якої невідомий. Для його визначення проведемо серію спостережень над величиною Т. При цьому Т набуде низку конкретних значень, що являють собою статистичний матеріал.

Якщо кількість даних перевищує 25, то для спрощення подальших розрахунків складають статистичний ряд. Для побудови статистичного ряду визначають зону розсіювання досліджуваної величини за формулою

R = t_max- t_min, (1)

де t_max і t_min – відповідно максимальне і мінімальне значення величини.

Потім визначають кількість інтервалів

n = 1+3.3lnN, (2)

де N – кількість дослідних даних (відмовлених виробів).

У практиці розрахунків рекомендується розглядати 7-20 інтервалів. Тому кількість інтервалів можна не розраховувати за формулою (2), а взяти в рекомендованих межах.

Знаючи зону розсіювання і число інтервалів, розраховують ширину (величину) інтервалу

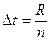(3)

Ширину інтервалів округлюють до цілих парних значень. Усі інтервали повинні бути однаковими, прилягати один до одного і не мати розривів.

Початок першого інтервалу визначається так, щоб мінімальне значення величини містилося приблизно на його середині. Останній інтервал вибирається таким, щоб максимальне значення величини потрапляло в цей інтервал.

Потім підраховують частоту відмов f_i випадкової величини у кожному інтервалі, накопичену частоту ∑f_i, частість (дослідну ймовірність) f_i/Nі накопичену частість ∑f_i/Nкожного інтервалу.

При підрахунку частоти f_i значення, що потрапляють на межу інтервалів, ділять порівну на обидва інтервали.

Накопичені частота ∑f_i і частість ∑f_i/Nдля кожного інтервалу визначаються як сума частот чи частостей усіх попередніх інтервалів. Для останнього інтервалу

∑f_i=N і ∑f_i/N =1.

Далі для наочної характеристики експериментального розподілу відмов будують гістограму і полігон (рисунок 1).

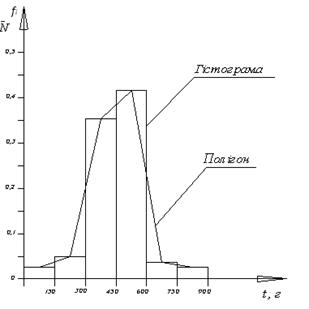
Рисунок 1 – Графічне оформлення статистичного ряду (гістограма і полігон)

Обчислюють статистичні характеристики розподілу випадкової величини за формулами:

а) середнє арифметичне

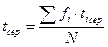, (4)

де t_{i cер} – середнє значення інтервалу;

б) середнє квадратичне відхилення

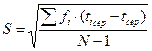при N<25, (5)

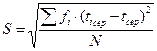при N≥25; (6)

в) дисперсіядорівнює S²;

г) коефіцієнт варіації

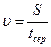(7)

Наступним етапом опрацювання дослідних даних є вибір теоретичного закону розподілу за коефіцієнтом варіації. Якщо υ=0-0,3, то вибирають нормальний закон розподілу, якщо υ=0,3-0,8 – закон Вейбулла, і якщо υ=0,80-1,30 – експоненціальний закон.

«Вирівнювання» емпіричного розподілу згідно з вибраним теоретичним законом полягає у визначенні теоретичних значень частот, частостей і накопичених частот чи частостей.

Лекція 8