Наращение при дробном числе лет.

Наращение по сложной процентной ставке при дробном числе лет может производится двумя методами: точным и смешанным.

Точный метод. Формула наращения сложных процентов, выведенная для целых положительных n, может применяться и для нецелых .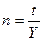

Пример. 13 января в банк положили сумму 1000$, до востребования под ставку 6% годовых сложных процентов. Какую сумму снимет вкладчик 1сентября.

Решение:

13 января - № 13; 1 сентября - № 244.

Следовательно t=244-13=231. PV=1000$; i=0,06.

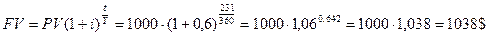
Смешанный метод наращения по сложным процентам. Если начисление процентов происходит за период, превышающий один год, и при этом период финансовой операции, выраженный в годах, является дробным числом, то с точки зрения инвестора (кредитора) наибольший эффект может быть получен при начислении процентов по смешанной схеме начисления процентов.

Смешанный метод (смешанная схема) начисления процентов – это такой метод, который предусматривает использование на разных временных интервалах различных схем начисления процентов. Такой метод позволяет комбинировать простые и сложные проценты с целью получения наибольшего эффекта. Формула наращения при этом имеет вид:

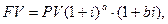(3.3)

где 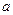- целое число лет;

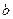- дробная часть года.

Эту формулу, как правило, используют в реальной банковской практике для финансовых вычислений.

Пример.Кредит в размере 3 млн. руб. выдан на 3 года и 160 дней под 16,5% сложных годовых. Найти сумму долга на конец срока двумя методами.

1) Точный метод:

.

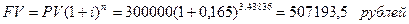2) Смешанный метод:

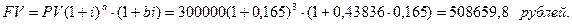
Как видим, смешанный метод дает более высокий результат.