Непрерывное наращение и дисконтирование
До сих пор мы рассматривали в качестве процентного периода некоторый фиксированный промежуток времени (год, квартал, месяц, день). Уменьшая этот промежуток (до часа, минуты, секунды) и увеличивая частоту начисления процентов, можно перейти к непрерывному наращению процентов.
Пусть номинальная годовая ставка равна i.
При начислении процентов 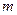 раз в году по ставке
раз в году по ставке 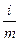 эффективная годовая ставка
эффективная годовая ставка 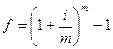
Таким образом, за год сумма увеличится в 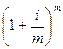 раз. При все более частом наращении процентов, т.е. при
раз. При все более частом наращении процентов, т.е. при  → ∞, используя второй замечательный предел, получим:
→ ∞, используя второй замечательный предел, получим:
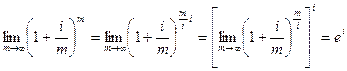
где 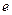 - число Эйлера (основание натурального логарифма),
- число Эйлера (основание натурального логарифма), 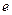
 2,718.
2,718.
Таким образом, непрерывным наращением по ставке 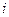 называется увеличение суммы
называется увеличение суммы 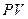 в
в 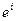 раз за один год или в общем случае в
раз за один год или в общем случае в 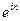 раз за
раз за 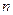 лет.
лет.
Процентную ставку, применяемую при непрерывном начислении процентов, называют сила роста и обозначают 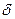 . Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени.
. Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени.
В общем случае, формула непрерывного наращения процентов имеет вид:
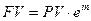 . (3.8)
. (3.8)
Для того чтобы отличить непрерывную ставку от дискретной, обозначим силу роста 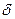 . Тогда формула непрерывного начисления процентов примет вид:
. Тогда формула непрерывного начисления процентов примет вид:
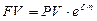 (3.9)
(3.9)
Эта формула верна и для случая, когда 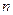 не является целым числом.
не является целым числом.
Пример. На сумму 10 000 рублей начисляются проценты по ставке 8% годовых. Определить наращенную сумму через 3,5 года.
Решение: 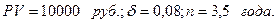
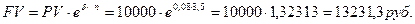
Используя формулу (3.9), можно получить формулу непрерывного дисконтирования:
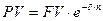 (3.10)
(3.10)
Пример.Какую сумму следует поместить на банковский депозит, чтобы через 5 лет получить 300 000 рублей, если проценты начисляются непрерывно по ставке 8%?
Решение: 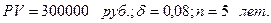
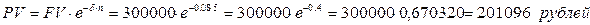
Дата добавления: 2015-10-26; просмотров: 2266;
