Сравнение множителей наращения по простым и сложным процентам
Для того чтобы выяснить, какой схемой начисления процентов целесообразно пользоваться при проведении долгосрочных и среднесрочных финансовых операций, и какой – при проведении краткосрочных, сравним величины множителей наращения по простым ( 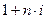 ) и по сложным
) и по сложным  процентам. Для этого выберем единый уровень процентной ставки, равный 10% годовых. Временной базой будем считать год, равный 365 дням. Значения множителей наращения занесем в таблицу.
процентам. Для этого выберем единый уровень процентной ставки, равный 10% годовых. Временной базой будем считать год, равный 365 дням. Значения множителей наращения занесем в таблицу.
| Способ начисления | Значение множителя наращения в зависимости от срока операции | ||||||
| 30 дней | 180 дней | 1год | 5 лет | 10 лет | 20 лет | 50лет | |
| Простые проценты | 1,00822 | 1,04932 | 1,10 | 1,5 | 2,0 | 3,0 | 6,0 |
| Сложные проценты | 1,00786 | 1,04812 | 1,10 | 1,61051 | 2,59374 | 6,72750 | 117,39085 |
Как видим, при 0 < 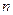 <1 имеет место неравенство
<1 имеет место неравенство  <
< 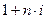 .
.
При 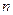 >1 – неравенство противоположного смысла:
>1 – неравенство противоположного смысла:  >
> 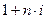 .
.
При 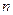 = 1 значения множителей наращения равны.
= 1 значения множителей наращения равны.
Отметим, что эти соотношения верны при любых значениях 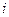 .
.
Таким образом, с точки зрения инвестора (кредитора) при долгосрочных финансовых операциях больший эффект достигается при применении сложных процентов, при краткосрочных операциях для наращения, с его точки зрения, выгоднее применять простые проценты.
Дата добавления: 2015-10-26; просмотров: 1352;
